If the above equation is differentiated using the product rule, it becomes
|
Heat and work represent two distinct means by which the internal energy of a system can change. In this article I clarify the fundamental, molecular differences between these two processes. Examples of both heat and work are abundant in everyday life. ice melts at room temperature because heat flows from surrounding air to the ice. Similarly, work must be done on gas in a piston to compress it. Both of these processes involve increasing the energy of the system. In fact, the first law of thermodynamics states that the change in internal energy of a system is equal to the amount of heat and work done. Interestingly, internal energy is a state function (it depends only on the present state of the system), while the heat and work are path functions (they depend on the process through which the change occurred). Thus for a reversible process, the first law is given by Where U is the internal energy, w is the reversible work, and q is the reversible heat. A very common form of work is pressure-volume work, such as compression. In this case the work can be expressed as Where P is the pressure and V is the volume of the system. Although it is easy to distinguish between examples of work or heat, it is less obvious how these quantities are fundamentally different. Consideration of the system on a molecular level will help with this. From this prospective, there are a variety of discrete energy states that the system can occupy. The macroscopically observed energy will be equal to the average energy of the system. From probability, the average value of a discrete random variable can be expressed as the sum of the product of each value and its respective probability. We can apply this to the internal energy of a macroscopic system since it’s allowed energy states are discrete. Where U is the macroscopically observed internal energy, p is the probability of the system being in state j and E is the state's energy. Do not worry about how the probability is determined yet, I discuss this in my article about temperatures below absolute zero. If the above equation is differentiated using the product rule, it becomes E is a function of the number of particles (N) and the volume (V). Since the number of particles is constant, dE can be viewed as the change in energy due to a small change in volume. This implies that This expression is analogous to the first law of thermodynamics! I restate this law below: The work (-PdV) must correspond to the first term above, because both are in terms of dV. Since there are only two terms, the second term must give the heat. Thus: This result finally shows how heat and work are different on the molecular level. Work changes the amount of energy that each allowed state has, without altering the probability distribution of the states (p is constant). Conversely, heat does not change the allowed energy states of the system (E is constant). Instead, it changes the probability distribution of the allowed states. They both change the average energy, but do so in different ways.
2 Comments
8/14/2013 06:08:52 am
Interesting! I never understood what the difference was until now!
Reply
ALAN EVANSON
10/19/2020 12:25:34 am
This is one of the most informative answers that I have ever read. How does the above analysis help explain electrical work? My understanding is that if a current runs through a resistor, electrical work is being done on the resistor, even though it will become hotter as if heat was applied. How can we use the above to explain that it is work and not heat that is being applied to the resistor?
Reply
Leave a Reply. |
Archives
April 2024
Categories
All
List of all articlesThe Tollens condensation
How long it takes chemical reactions to reach completion Benzocaine synthesis Mathematics of compound interest Dynamic nuclear polarization in solid state NMR Modelling a multi-state G protein signalling pathway Organic synthesis of Aspirin Distinguishing enzyme inhibition mechanisms Metformin total synthesis Ki, Kd, IC50, and EC50 values AZT: mechanism and synthesis Forecasting website ad revenue Km vs Kd The relationship between TV screen size and price Health benefits of green tea Synthesis of ibuprofen from benzene The mechanism of action of Eflornithine Synthesis of sucralose from sucrose Diluting a solution to Avogadro's limit The affect of mutation rate on evolutionary equilibrium Organic synthesis of indomethacin Probing protein-protein interactions in the yeast glycolytic metabolon Time course enzyme kinetics A generalized model for enzymatic substrate inhibition The basis of high thermostability in thermophilic proteins First order drug elimination kinetics Improving the efficiency of protein dialysis: constant dialysate replacement Mathematical modelling of evolution Calculating the optimum ddNTP:dNTP ratio in Sanger sequencing A mathematical model of hair growth Life does not violate the second law of thermodynamics Collagen and the importance of vitamin C Temperatures below absolute zero are surprisingly hot The molecular difference between heat and work |
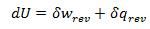
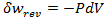
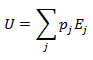
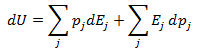
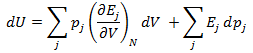
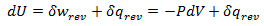
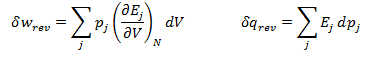
 RSS Feed
RSS Feed