My goal is to develop simple equations to describe the curves that result from these calculations. The typical person has of the order of a hundred thousand hairs on their head. Hence by the Law of Large Numbers the probabilistically expected result will be identical to the actual result. Thus, I will model this situation by computing the probabilistically expected results.
Average hair length at equilibrium
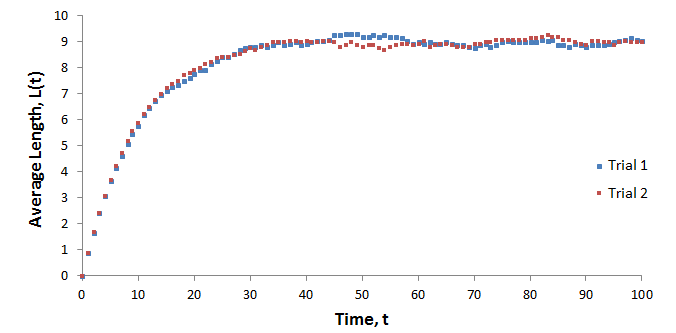
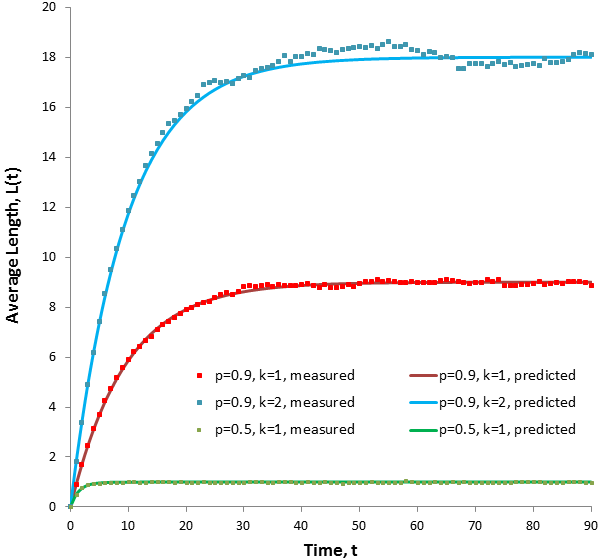
Average hair length as a function of time
At what time is equilibrium reached?
The distribution of hair lengths at equilibrium
When thinking about the visually apparent length it is more useful to instead consider the distribution of lengths seen in the population of hairs. The numbers of hairs in each length state follow an exponential decay curve as the length of the state increases. This follows from what I had already shown regarding the probability of each length state earlier. For simplicity, let q be the complement of p: q=1-p.
First, I will derive an equation for the number of hairs in each length state when the system has reached equilibrium [i.e. L(t)=M]. The state i=0 has a length of 0. Recall that in a given time interval all hairs have a probability of q of falling out, of switching to the i=0 state. Note that this applies even to the i=0 state itself, a proportion of q of the hairs in the i=0 state will stay in this state over a given time interval. Thus the number of hairs in this state will be Nq, where N is the total number of hairs. Now consider the i=1 state. A proportion of p of the Nq hairs at i=0 will grow to the i=1 state. We needn’t consider the number of hairs previously occupying this state, as all either grow to the i=2 state or fall out and return to the i=0 state. Thus the number of hairs at the i=1 state are Nqp. This logic can be applied again to show that there are Nqp^2 in the i=2 state, Nqp^3 in the i=3 state, and so forth. In general:
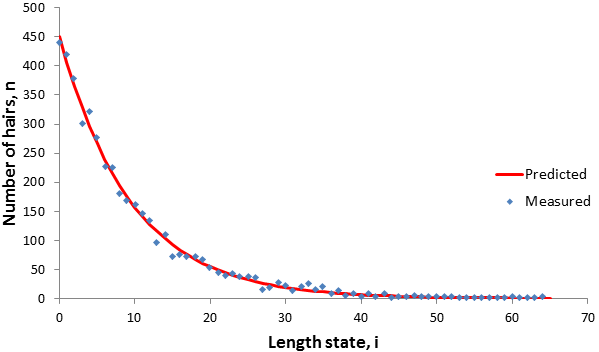
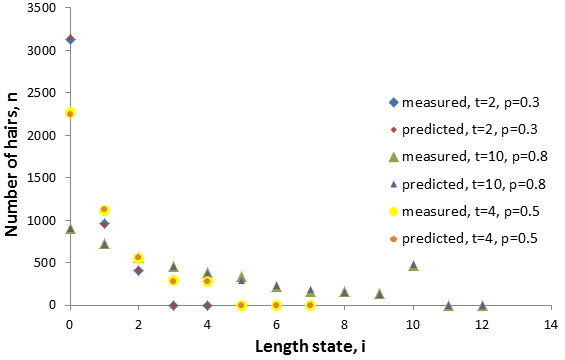
This model is consistent with the distribution I observe in simulated data. For instance, at equilibrium with N=4500 and p=0.9:
The distribution of hair lengths as a function of time
However, the i=t state is the highest accessible length state to the population. Here we must consider all hairs which transiently reached this state. We needn’t worry about the number which will leave in this iteration since there are no hairs initially occupying the state. Thus, the number is simply Np^t.
Should this argument not convince you, here is an alternative way of demonstrating this. We can consider two contributions to the number of hairs in the state i=t. Firstly, the normal Nqp^i term, but also the sum of all hairs which at later time will further distribute themselves among the higher length states at equilibrium:
The size of the peak when p>0.5 would of course increase with p, and vice versa for when p<0.5. In the case of human hair, recall that the number of hairs of a typical person is of the order of 10^5. A generous estimate for the number of hairs falling out per day is 100. Thus the p value would be of the order of 0.999 per day. Also, as I have argued before, the typical person’s hair is far below its equilibrium length. Therefore, the equation implies that typical human hair has a large peak in the distribution at the maximum length state, i=t. In other words, the majority of a typical person's hairs have the same length, with very few having shorter lengths. Upon inspecting your own head you will likely notice that most of your hairs have roughly the same length. Of course this illustration is complicated by unequal cutting of different regions during a haircut, but this works well focusing locally on a small region.
The intended application of the model I have developed is hair growth. However, it also applies to a wide variety of other situations, any which satisfy the assumptions made by the model. For instance, my results that could be applied to the heights of trees in a forest. The model would require that each tree cut down is replanted and that the selection of trees is independent of their height. Small modifications to the model could be done so that it more appropriately fits other situations. In the case of a forest, we may want to add a factor to make the cutting of trees biased towards taller ones, for instance.
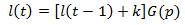
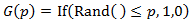
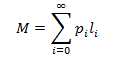
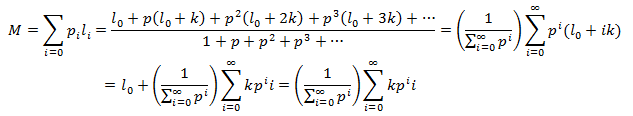
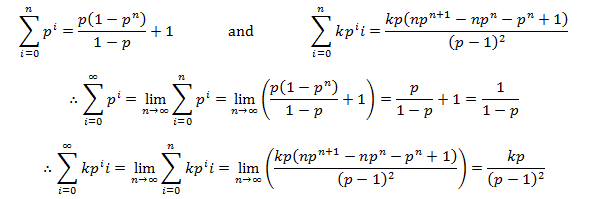
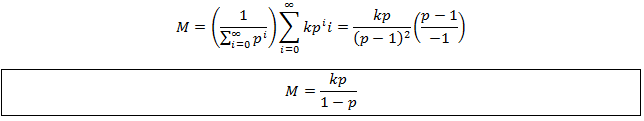
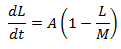
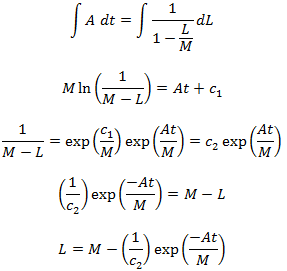
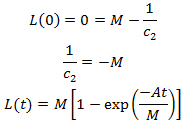
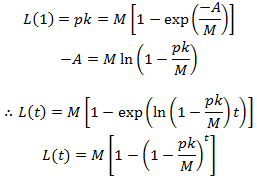
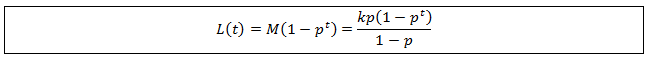
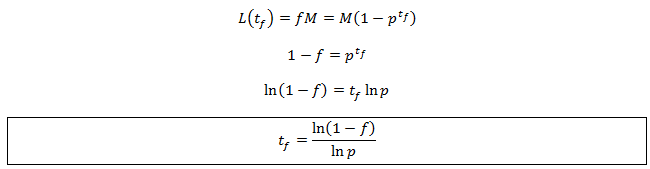
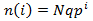
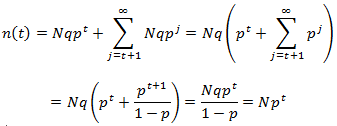
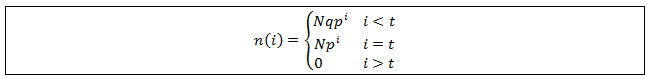
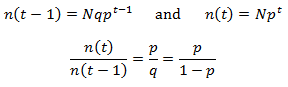
 RSS Feed
RSS Feed