The dissociation constant (Kd)
The Michaelis constant (Km) and the Michaelis-Menten equation
The rapid equilibrium derivation
The steady-state derivation
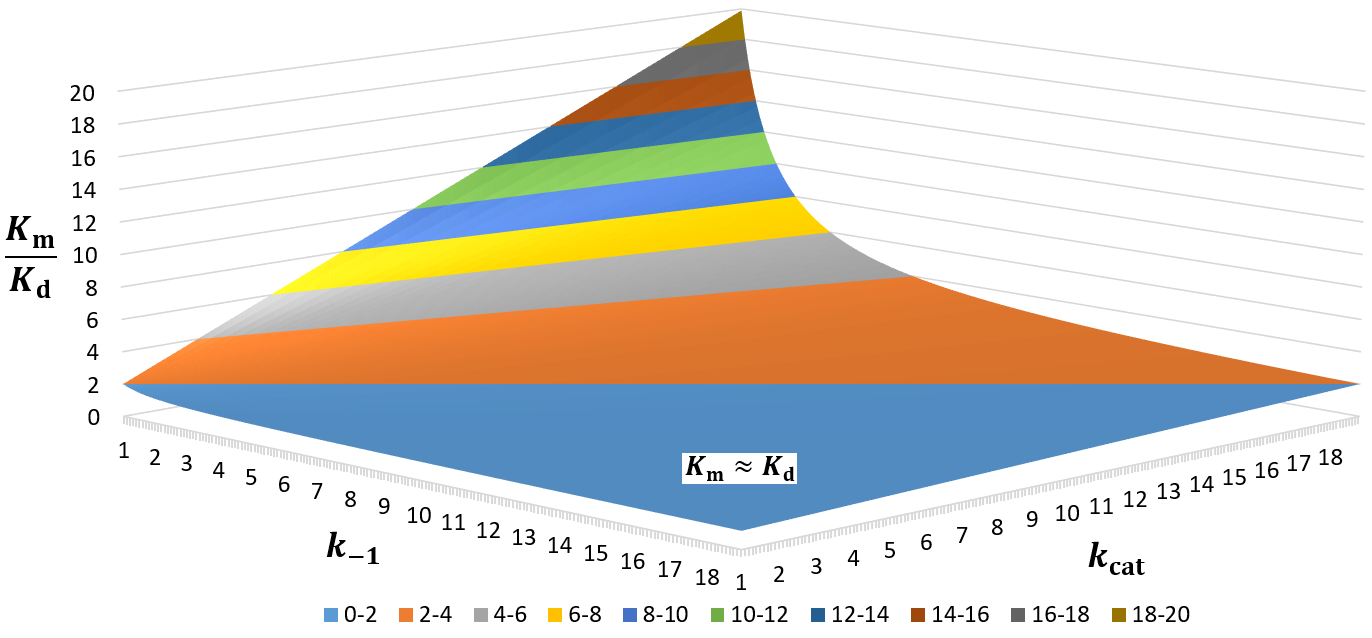
The difference between Km and Kd
Because Km is related to Kd, people often take this parameter to be a measure of binding affinity. It does provide information about this, but assuming they are equivalent is a common and problematic fallacy. It is impossible to know whether the rapid equilibrium assumption is obeyed from simple Michaelis-Menten kinetics alone. In extreme cases, taking Km to approximate Kd might underestimate the substrate’s binding affinity by orders of magnitude. To demonstrate this, we can evaluate the difference between Km and Kd by calculating their ratio.
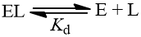
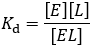
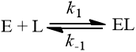
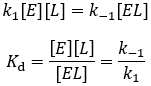
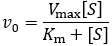
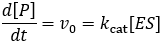
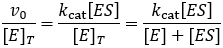
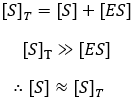
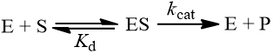
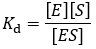
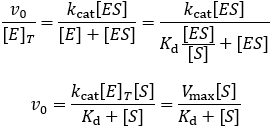
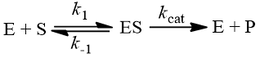
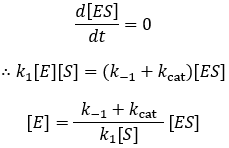
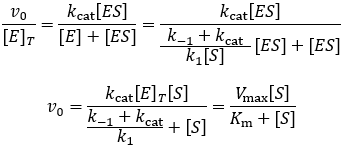
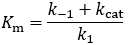
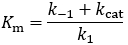
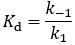
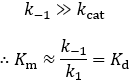
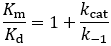
 RSS Feed
RSS Feed