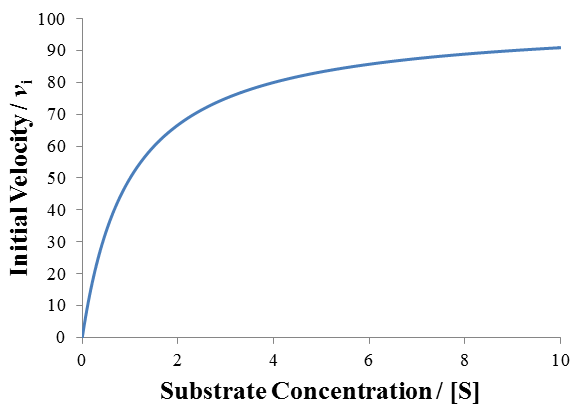
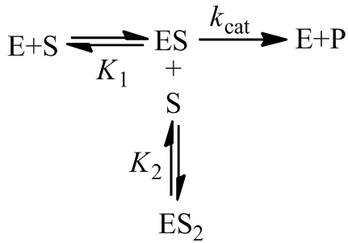
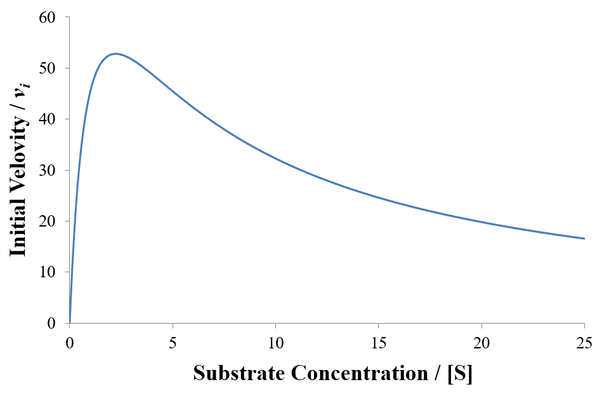
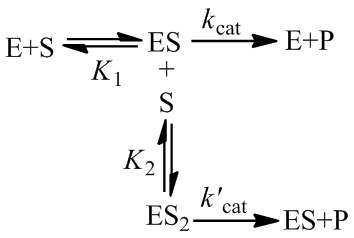
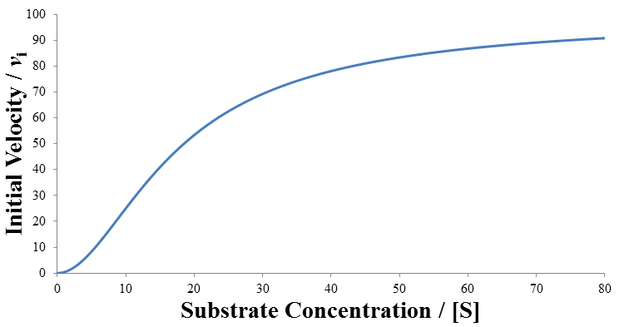
Although many enzymes are described well by the Michaelis-Menten equation, many require more complex models. One such deviation is substrate inhibition. In this case, the enzyme must have at least two binding sites for the substrate. Typically, binding of the first substrate results in a catalytically active enzyme. However, if the enzyme is subject to substrate inhibition, the binding of an additional substrate to the other binding site results in a catalytically inactive enzyme. Where the goal of enzymes are to speed up the rates of reactions in biological systems, it may seem at first strange and counter-productive for an enzyme to be inhibited by its own substrate. This certainly has the potential to greatly reduce or completely halt catalysis. Biological systems are highly ordered, it is not sufficient for all reactions to always proceed as quickly as possible. Instead, the rates of reactions must be highly regulated to facilitate processes like homeostasis. Substrate inhibition is therefore used as an important regulatory mechanism used by a variety of enzymes to achieve different ends. For instance, phosphofructokinase is an important enzyme in glycolysis, a bioenergetically essential process where energy is liberated from glucose in the form of ATP. Although there is net gain of ATP over glycolysis, an essential step is the phosphorylation of fructose 6-phosphate using ATP. Phosphofructokinase catalyzes this conversion. Interestingly, phosphofructokinase shows substrate inhibition with respect to ATP. The regulatory function of this is clear: glycolysis is not needed if there is already sufficient abundance of ATP in the cell. When there is ample supply of ATP, substrate inhibition on phosphofructokinase blocks further glycolysis. Conversely, as ATP concentrations fall there is less substrate inhibition and the rate of glycolysis increases. This is merely one example, there are many well understood and distinct examples where substrate inhibition acts as a physiologically significant regulatory mechanism. For a more detailed discussion and additional examples see this article.
Classical Substrate Inhibition
A Generalized Description of Substrate Inhibition
General Equation for Optimum Substrate Concentration
Intuitively, it is clear that [S]* is undefined when V2 > V1. In this case, binding of the second substrate molecule is activating and thus maximum activity is approached asymptotically towards infinite substrate concentration. Hence, there is no defined maximum. It is also possible to show this mathematically. Let us think back to the more general form of the solutions to the quadratic equation:
Special Cases of the Substrate Inhibition Equation
In the special case where the enzyme bound to a single substrate is active, but completely inactive when two substrate molecules are bound (that is, V1max > 0, V2max = 0). Of course the general equation simplifies to give the markedly simplified result obtained earlier.
In the special case where the enzyme bound to a single substrate is inactive, but active when two substrate molecules are bound (that is V1max = 0, V2max > 0). Formation of the ES complex has the effect of decreasing the “apparent Km” of the enzyme, it partitions a fraction of the enzyme population into an inactive state in the presence of substrate. This effect is not truly simply increasing the Km value though, as the situation is no longer classical Michaelis-Menten kinetics:
Special Case III: No Cooperativity (K1 = K2 = Km)
In this case, the enzyme exhibits no cooperativity with respect to substrate binding; binding the first substrate has no effect on the enzyme’s affinity for the second. Furthermore, the binding sites for the two substrates would likely be symmetric. By making the substitution K1 = K2 = Km, we obtain a simplified equation for the optimum substrate concentration:
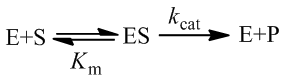
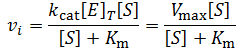
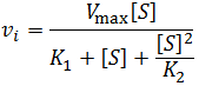
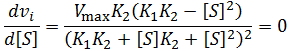
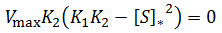
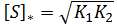
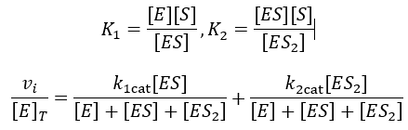
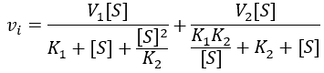
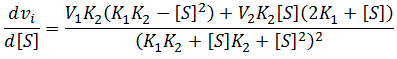
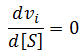
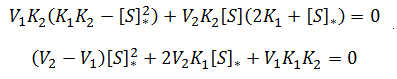
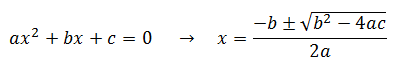
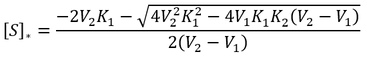
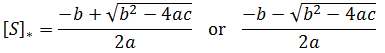
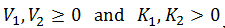
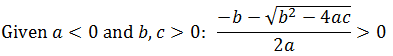
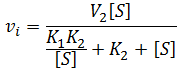
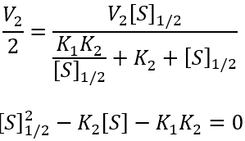
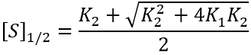
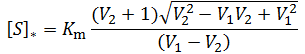
 RSS Feed
RSS Feed