Two commonly encountered parameters in enzyme kinetics are the Michaelis constant (Km) and the dissociation constant (Kd), both report aspects of a substrate’s binding behavior. In this article, I clarify these terms' definitions, differences and biochemical significance. Though related to each other, Km and Kd are not the same. To clarify this, I review two ways the Michaelis-Menten equation can be derived: the rapid equilibrium assumption and the steady-state approach.
The dissociation constant (Kd)
The dissociation constant (Kd) quantifies the equilibrium between a ligand (L) being free in solution and bound to a site in a protein (EL):
It corresponds to the affinity which the ligand has for the binding site. Ligands with higher, more favorable free energy of association bind “tighter” and therefore have greater preference for the bound state. Because Kd is defined as a dissociation constant, higher affinity ligands have lower Kd values. As an equilibrium constant, we can express it as the ratio of product concentrations over reactants:
Alternatively, we can interpret the Kd equilibrium kinetically, through association (k1) and dissociation (k-1) rate constants:
Equilibrium is reached when ligand binding and dissociation occur at equal rates:
Therefore, Kd is equal to the ratio of the dissociation rate constant (k-1) and the association rate constant (k1). Dissociation is a unimolecular process, while association is bimolecular, accounting for the molarity unit of Kd.
The Michaelis constant (Km) and the Michaelis-Menten equation
The Michaelis-Menten equation is the most widely known model in enzyme kinetics:
Where v0 is the initial reaction rate, [S] is the substrate concentration, Km is the Michaelis constant, and Vmax is the maximum reaction rate. The Michaelis constant describes the kinetics of substrate/enzyme binding. However, its precise meaning depends on what assumptions are made when deriving the equation. Reviewing the derivations of the Michaelis-Menten equation is essential to clarify this. We begin by expressing the rate of product formation (v0). By definition, the enzyme converts bound substrate (ES) into product through first order rate constant kcat.
This is not a very useable form of this equation, it is experimentally hard to know how much enzyme-substrate complex has formed. It much more feasible to know the total enzyme concentration, [E]T. Therefore, we aim to get the equation in terms of this. We can start by dividing both sides of the equation by this term.
Now we must develop expressions for the concentrations of enzyme-substrate complex (ES) and free enzyme (E) in terms of quantities we know or can measure. A few assumptions are required to do this. Firstly, it is helpful that the total enzyme concentration is usually much smaller than the substrate concentration. This lets us make the simplifying assumption that depletion of substrate by binding the enzyme is small and so the free substrate concentration (S) is well approximated by the total (ST):
This alone is not enough though, to obtain the Michaelis-Menten equation we must also make either the rapid equilibrium or the steady-state assumption.
The rapid equilibrium derivation
Under the rapid equilibrium assumption, we assume that the rate at which the equilibrium is established for substrate binding is fast compared to the rate at which the ES complex forms product. Therefore, the substrate binding step can be described by its equilibrium dissociation constant (Kd).
Many enzymologists refer to this dissociation constant as Ks, for “substrate dissociation constant”. Despite the different terminology, its meaning is entirely identical to Kd as described above. For clarity, in this article I refer to this constant only as Kd. To derive the Michaelis-Menten equation, we describe the kinetics of substrate binding using its dissociation constant:
We can solve this equation for [E] and substitute it into our initial velocity equation:
The kcat and total enzyme concentration terms are grouped together and termed “Vmax” to represent the maximum substrate turnover rate the enzyme can catalyze. Comparing this result to the general form of the Michaelis-Menten equation, we can see that this assumption gives a Michaelis constant equal to the dissociation constant (Kd = Km).
The steady-state derivation
The steady-state assumption is a more general, alternative assumption we can make to derive the Michaelis-Menten equation. Here we assume that the concentration of the enzyme-substrate complex does not change much over the course of the reaction. More precisely, that its change is small compared to the rate of product formation. We must now describe substrate binding/dissociation through their respective rate constants, k1 and k-1.
Assuming that [ES] concentration is constant provides another method to develop an expression for free enzyme concentration [E]:
Now substituting this into our initial velocity equation:
Comparison of this result to the Michaelis-Menten equation reveals a more complicated definition of the Michaelis constant:
In this case, The Michaelis constant need not be equal to the dissociation constant. I clarify the details of this in the next section.
The difference between Km and Kd
We have seen that under the rapid equilibrium assumption, Km and Kd must be identical. An unsurprising result, since this approximation directly assumes that this is so. However, a broader definition of the Michaelis constant is afforded by the steady-state derivation.
The relationship between Km and the Kd may not be immediately obvious from this, but recall that we can express Kd as the ratio of the substrate dissociation/association rate constants:
The only difference between the Km and Kd expressions is the presence of kcat in Km’s numerator. Thus, whether Km is equal to Kd depends only on the relative size of k-1 and kcat. They are equal when k-1 is much larger than kcat.
This condition provides a more precise way of thinking about when the rapid equilibrium assumption is valid: when the chemical step (kcat) is slow compared to substrate dissociation (k-1). Whenever this condition is not met, the Michaelis constant will be larger than the dissociation constant. Since the turnover number (kcat) is a positive number, the Michaelis constant is always larger than or equal to the dissociation constant.
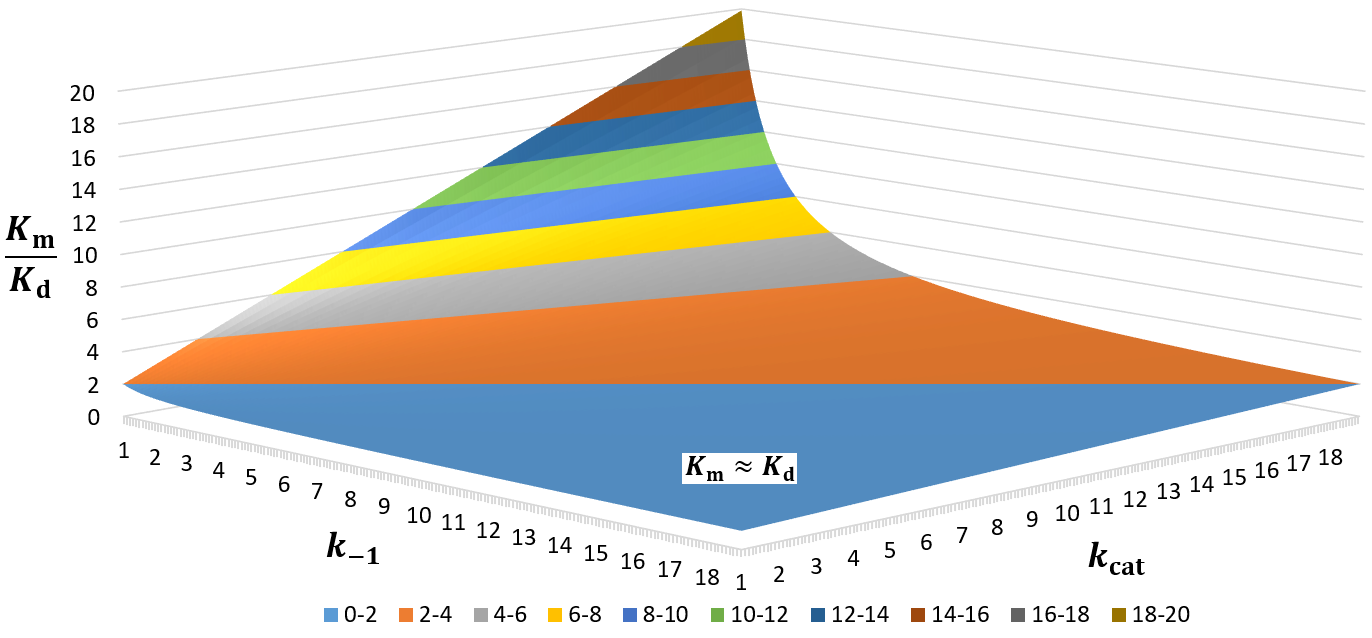
Because Km is related to Kd, people often take this parameter to be a measure of binding affinity. It does provide information about this, but assuming they are equivalent is a common and problematic fallacy. It is impossible to know whether the rapid equilibrium assumption is obeyed from simple Michaelis-Menten kinetics alone. In extreme cases, taking Km to approximate Kd might underestimate the substrate’s binding affinity by orders of magnitude. To demonstrate this, we can evaluate the difference between Km and Kd by calculating their ratio.
Because Km is related to Kd, people often take this parameter to be a measure of binding affinity. It does provide information about this, but assuming they are equivalent is a common and problematic fallacy. It is impossible to know whether the rapid equilibrium assumption is obeyed from simple Michaelis-Menten kinetics alone. In extreme cases, taking Km to approximate Kd might underestimate the substrate’s binding affinity by orders of magnitude. To demonstrate this, we can evaluate the difference between Km and Kd by calculating their ratio.
Interestingly, the substrate association rate (k1) cancels out from this equation. The size of the deviation is entirely a function of the relative size of kcat and k-1. To visualize this relationship, I plot Km/Kd as a function of kcat and k-1 as a 3D surface plot below.
Only in the indicated section (light blue), where k-1 > kcat, are the Km and Kd values similar. Thus, much of the possible kcat and k-1 space gives Km values far larger than Kd. This is worth remembering when interpreting kinetic data.
The biochemical meaning of Km vs Kd
I conclude by comparing the physical significance of these constants. The dissociation constant is a thermodynamic parameter and reports the true affinity a ligand has for binding a site on a protein. Furthermore, under usual conditions the dissociation constant gives the ligand concentration at which half of the protein molecules have ligand bound. In contrast, the Michaelis constant is a kinetic parameter, not an equilibrium constant. It gives the substrate concentration at which half of the maximum enzymatic reaction rate is attained. It is determined not only by the substrate’s binding affinity, but also by how quickly the enzyme-substrate complex is turned over into product.
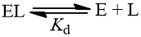
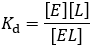
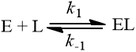
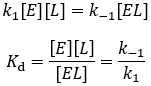
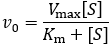
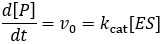
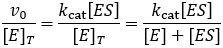
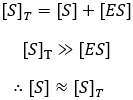
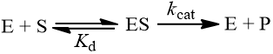
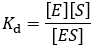
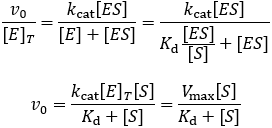
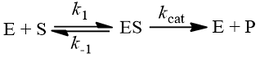
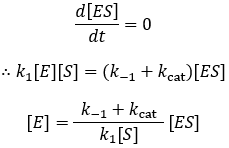
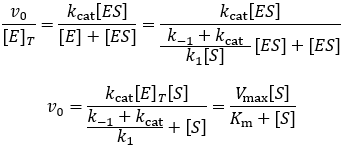
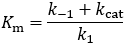
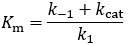
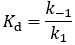
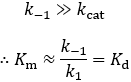
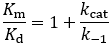
 RSS Feed
RSS Feed