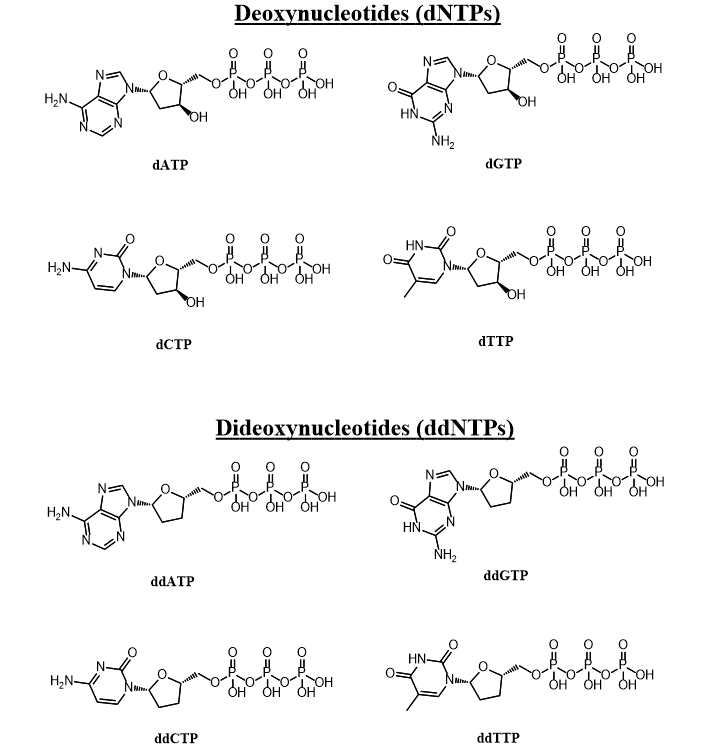
The ratio of dNTP to ddNTP used is critical for the success of Sanger sequencing since it determines the distribution of DNA fragment lengths produced. Despite this, I have been unable to find a detailed mathematical treatment of how this ratio affects the results. Thus, in the article I will explore the mathematical relationship between the dNTP to ddNTP ratio and the distribution of fragment lengths, and develop an equation to predict the optimum ratio under specified conditions. The accuracy of this model depends on the validity of the assumptions which I have made to develop it:
- The reaction goes fully to completion, all dNTP and ddNTP are used up, all strands being synthesized are terminated.
- The kinetics for the incorporation of a dNTP or a ddNTP are identical, both processes have identical rate constants.
- The DNA sample contains roughly the same amounts of guanosine, cytidine, adenosine, and thymidine, thus each nucleotide type will have the same optimum ratio of dNTP to ddNTP.
- The DNA sample being sequenced is long such that the fraction of fragments produced spanning the entire sequence is small.
- The separation from gel electrophoresis is ideal.
- No complicating secondary structure of DNA exists during sequencing.
We can define p as the fraction of nucleotides triphosphates derivatives which are normal dNTP:
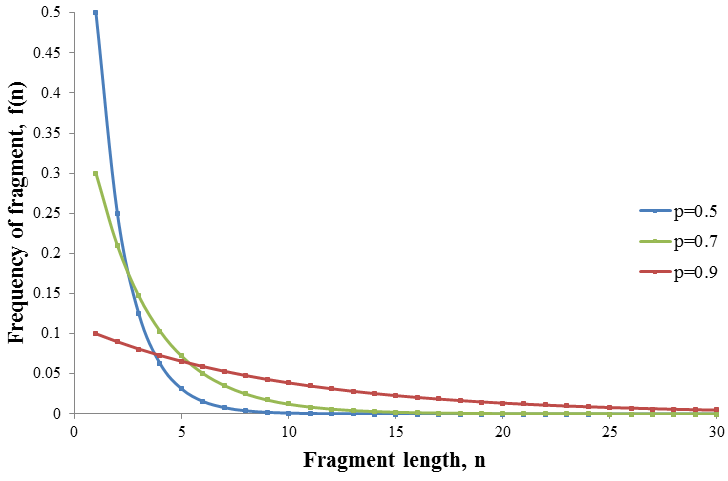
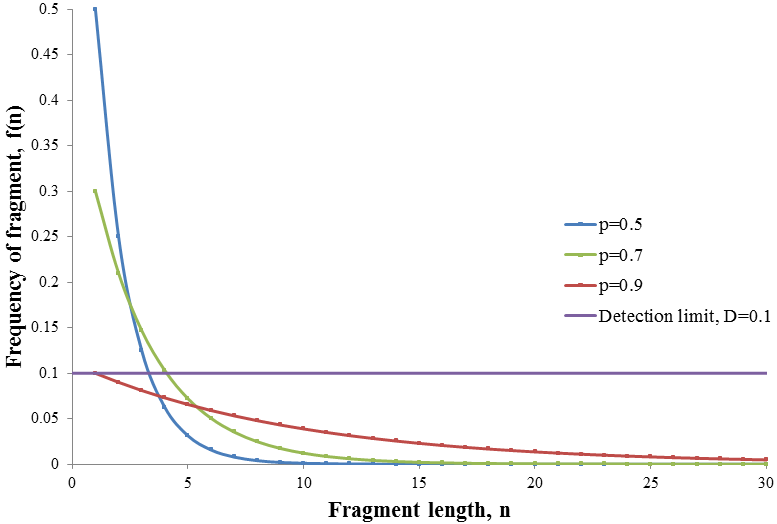
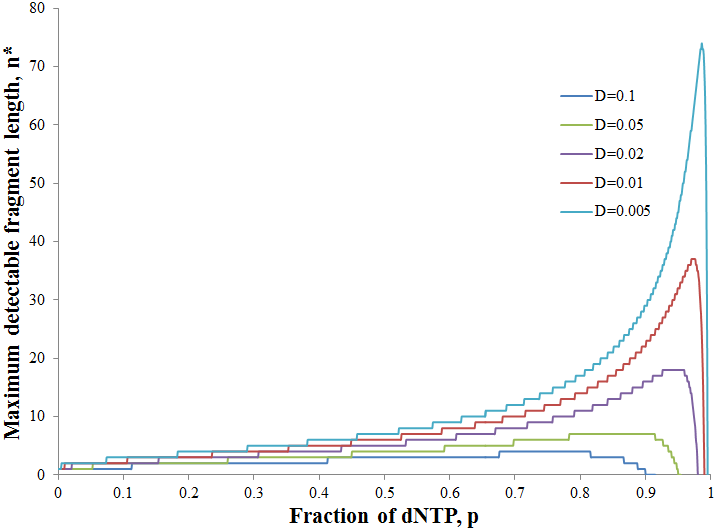
Note that f(n) is always maximum at n=1 (because p<1) and each term is successively smaller than the last. Thus for any distribution the number of detectable fragments will be equal to the length of the longest detectable fragment (n*). This length has the lowest frequency which is still above or equal to the detection limit:
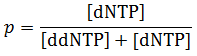
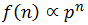
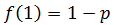
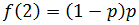
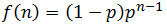
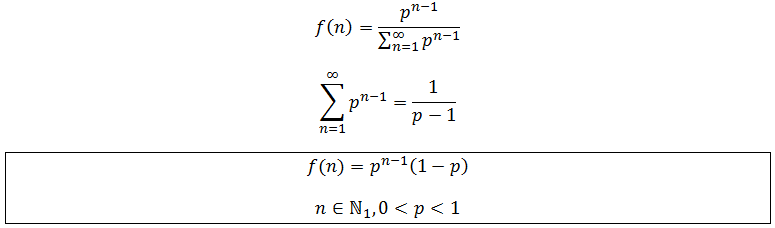
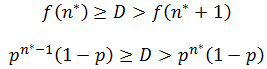
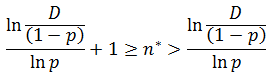
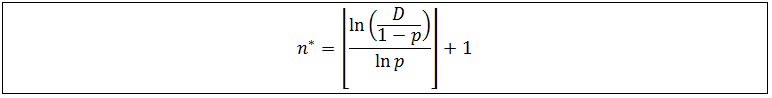
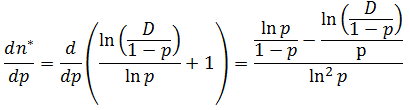
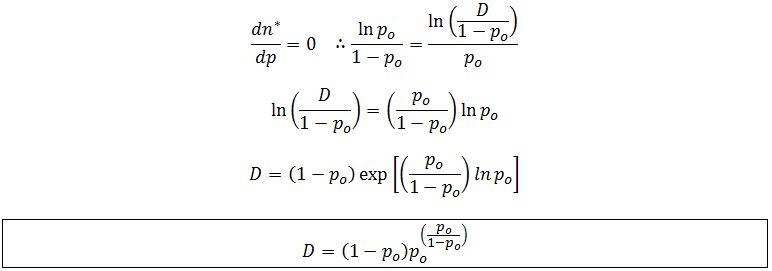
 RSS Feed
RSS Feed