In this article I develop equations to describe the progress of dialysis of a protein sample with respect to time. Through this, I demonstrate how the traditional dialysis protocol can be modified to maximize the rate of dialysis and minimize the volume of dialysate used. Traditional dialysis procedures involve having a dialysate volume much greater than that of the sample (typically at least 100x) and replacing it a one or more times with fresh dialysate. In contrast, I suggest placing the dialysis bag in a low-volume chamber with good mixing. Instead of replacing the dialysate a few times during the entire procedure, it is continuously exchanged by a constant flow of fresh dialysate through the chamber.
Dialysis without dialysate replacement
Suppose that we have a protein sample of volume VS in a dialysis bag, submerged in a volume VD of dialysate. During dialysis, the contaminant concentration in the sample decreases as it diffuses across the membrane into the dialysate. This net transfer occurs until equilibrium is reached where the dialysate and the sample contain the same concentration of contaminant. The rate of transfer is proportional to the concentration gradient, the difference between the concentration of contaminant in the dialysate and the sample. Equivalently, it is proportional to the difference between the sample’s concentration and the concentration at equilibrium. I assume that the rate constant (k) for diffusion across the membrane is an intrinsic property of the membrane, independent of the sample volume. Thus:
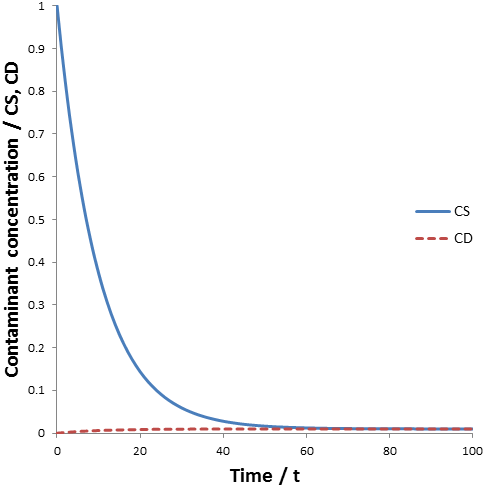
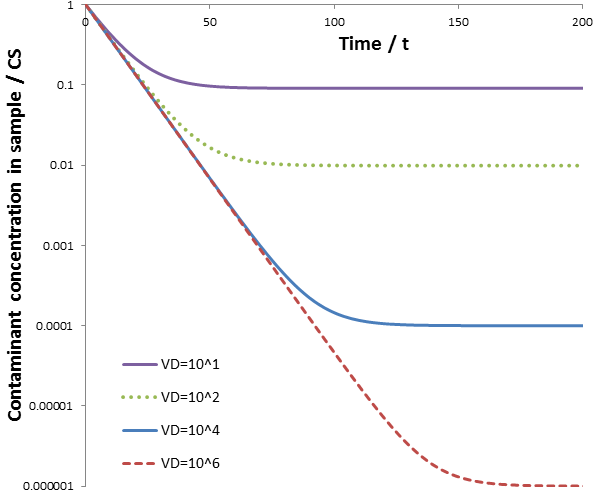
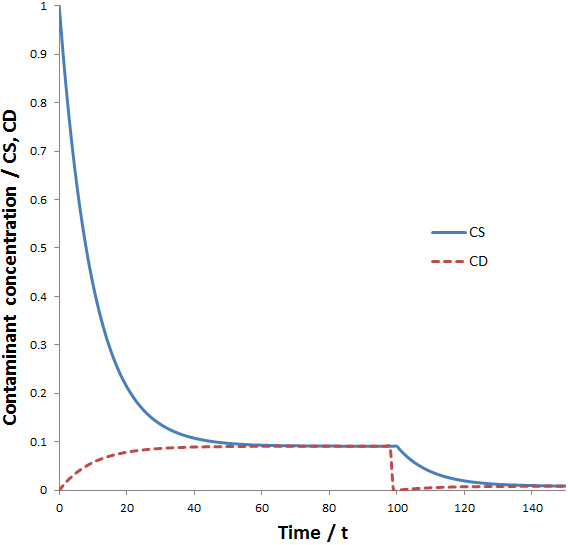
The figure below shows the contaminant concentration in the sample and the dialysate as a function of time given: CS(0)=1, CD(0)=0, VS=1, VD=100, and k=0.
Dialysis with discrete dialysate replacements
A commonly used strategy to overcome these issues is to replace the dialysate with the same volume fresh dialysate one or more times throughout the procedure. When the dialysate (at t=tC) is changed (at t=tc) the equilibrium concentration of the system is reduced since all of the contaminant in the dialysate is removed from the system:
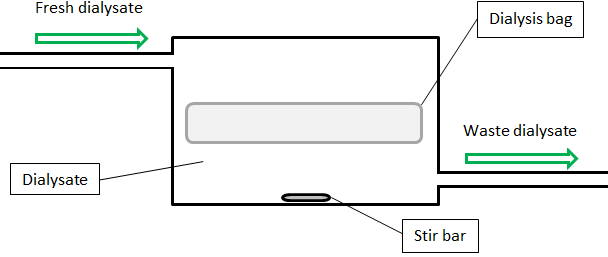
Dialysis with continuous dialysate replacement
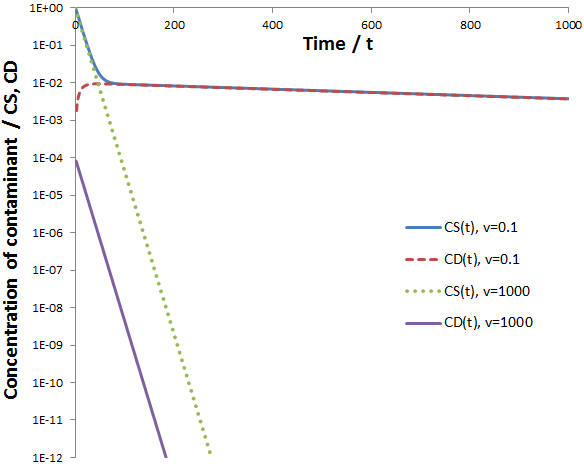
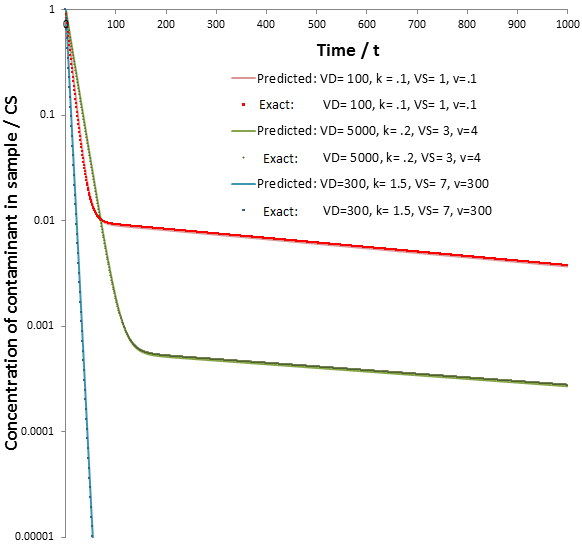
Given a very high flow rate, the dialysate is replaced so quickly that the contaminant does not have time to accumulate. That is, throughout the procedure:
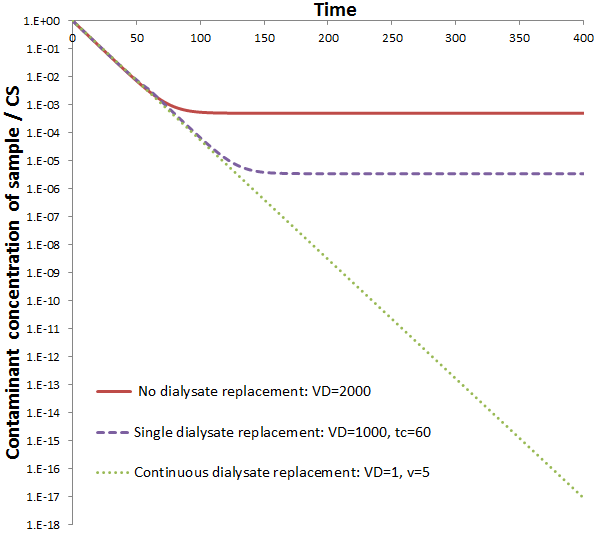
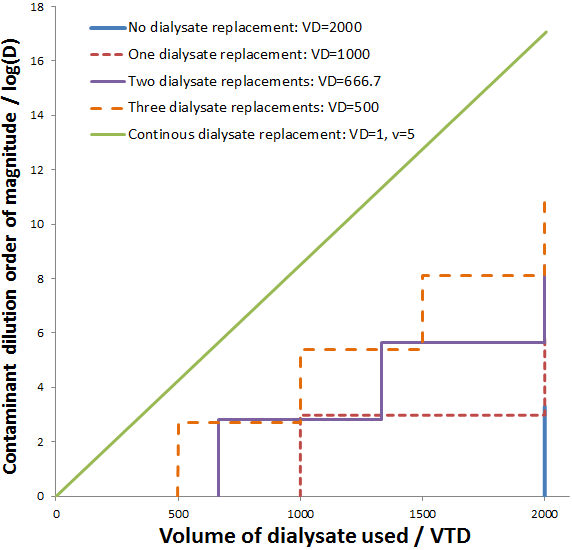
Impressively, this high rate of dialysis is attained while using a smaller volume of dialysate. The dilution of contaminant obtained for continuous dialysate is compared to discrete dialysate replacements below. The maximum dilution obtainable is plotted for the discrete dialysate replacements (given the system reaches equilibrium before the replacement). This is calculated, as before, according to:
This modification, continuous dialysate replacement, therefore is superior to the traditional dialysis protocol with respect to both the rate and the amount of dialysate used. The disadvantage is that a relatively complex apparatus is needed, which could be quite expensive to construct. However, once built the procedure could be automated by computer, requiring even less human intervention than the traditional protocol where manually changing the dialysate is necessary. My modification could be particularly useful for the purification of relatively unstable proteins, since it may decrease the time needed to attain a given dilution factor of contaminant. This strategy could also be especially beneficial when purifying proteins on an industrial scale. In this case, very large volumes of dialysate would be used. Thus, the decrease in dialysate volume required by this approach could be quite significant, potentially lowering the cost considerably.
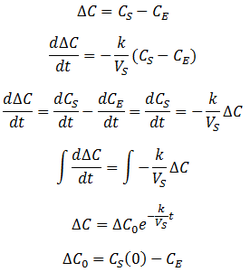
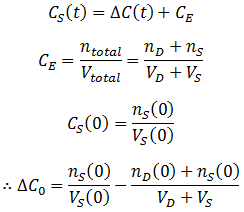
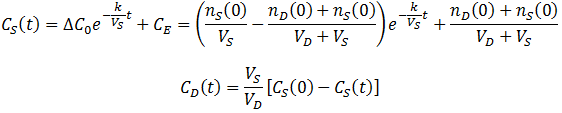
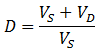
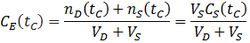
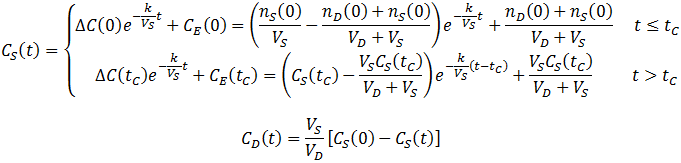
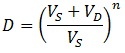
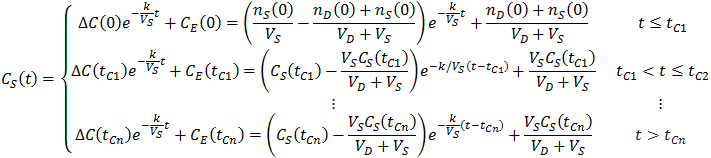
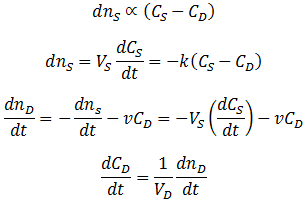
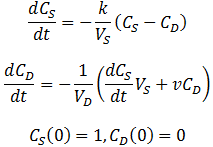

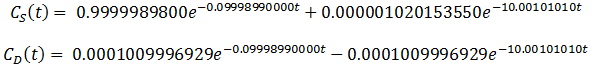
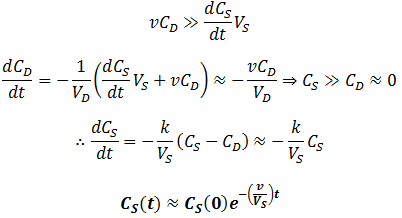
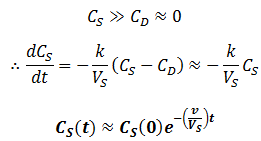
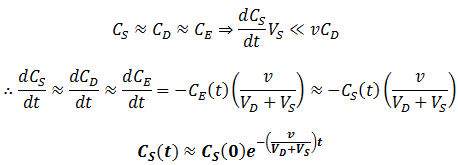
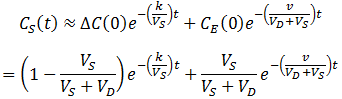

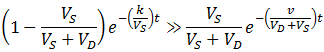
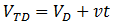
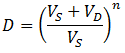
 RSS Feed
RSS Feed