Why do enzymatic reaction velocities decrease over time?
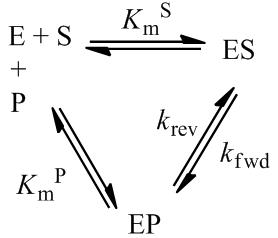
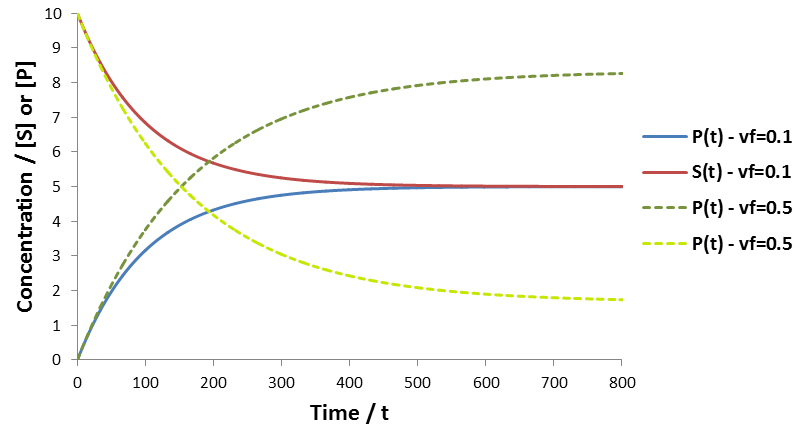
Nevertheless, numerical integration is another approach to this and is quite straight-forward to implement. There are also numerous software packages available with can automate this process, such as Mathlab or Excel. In evaluating this numerically, we can define the initial concentration of substrate as [S]0 and the amount that has been used up at time t as the product concentration [P](t). This assumes a 1:1 reaction stoichiometry and that [P](0) = 0. This allows us to write a time course velocity equation:
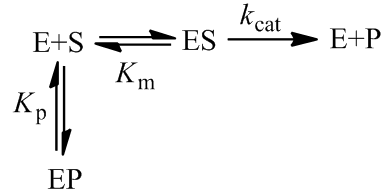
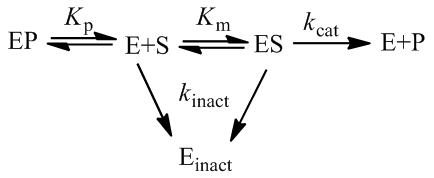
There are many situations where an enzyme may be inactivated through kinetics more complicated than as presented here. For instance, these equations make the assumption that the free enzyme and the enzyme-substrate complex inactivate at the same rate, which likely is not entirely true. The free energy of substrate binding generally contributes favourably to the overall free energy of folding of the protein and so in practice the rate of kinact to may be slightly slower for the ES complex. At the cost of the model’s simplicity, we could correct for this complication by giving the E and ES complex different rates of inactivation.
Exponential solutions to enzymatic time course kinetics
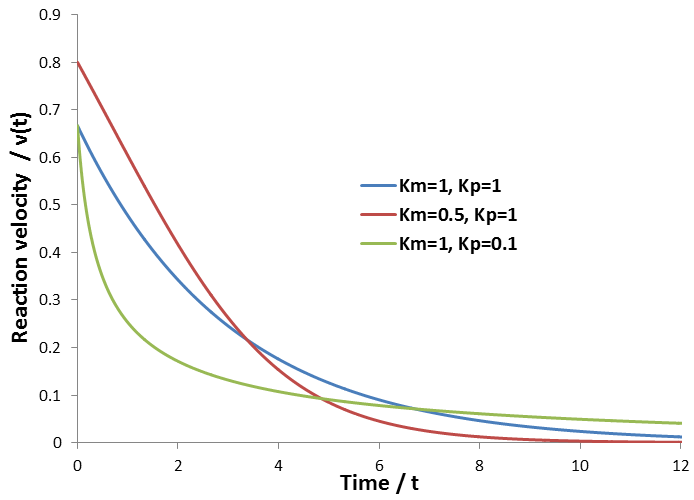
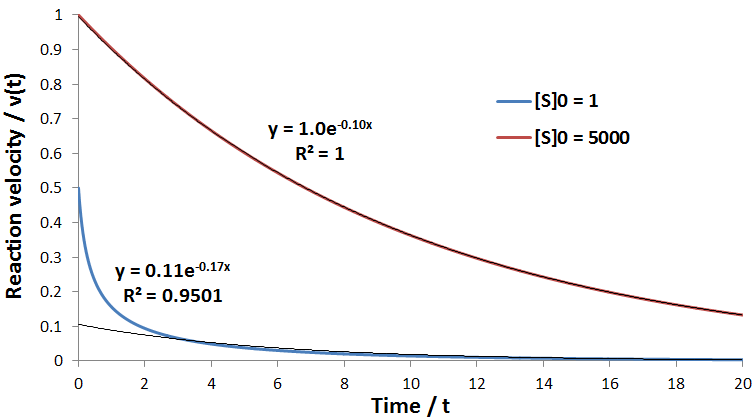
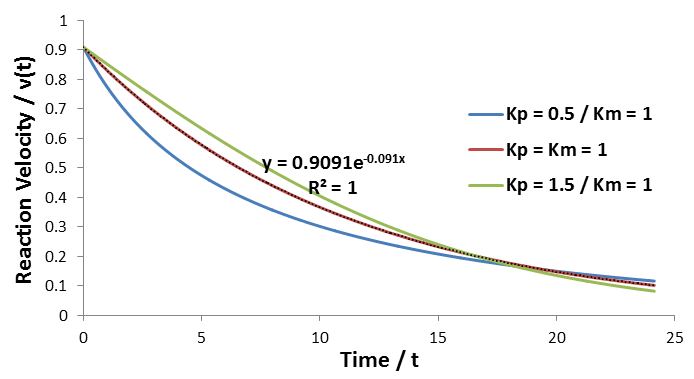
The relationship between the A and B coefficient when Km = Kp affords a convenient test for consistency of data with this model. Of course during any enzyme assay the initial concentration of substrate, [S]0, is known. As seen for the simulated data, the ratio between these coefficients must be equal to [S]0:
As in the previous case, the relationship the ratio between the A and B coefficients allow a convenient test for the consistence of data with this model. This ratio must be related to the initial substrate concentration by:
Integration of all factors into single model
The advantage of initial rate kinetics is its mathematical and conceptual simplicity. Time course kinetics requires significantly more complicated models and analysis. Further, more assumptions must also be made about the properties of the system. The high number of parameters is certainly a limitation of time-course kinetic analysis. The risk of selecting an inappropriate model and analysis of the data is significant, and considerable care with regard to this is required. Nevertheless, a wealth of information about the system is afforded by this technique. In particular, the rate of catalysis, binding affinity of the enzyme for the substrate and product, and the rate of enzyme inactivation are available directly from a single reaction. Using initial velocities alone, determination of all of these parameters would require at several distinct experiments performing many reactions over a range of substrate/product concentrations and incubation times. Though enzymologists normally disregard the data following deviation from initial velocity, I argue that this practice wastes insightful data. I suggest that initial velocity and time course experiments needn’t be distinct. Given time course kinetic data we can calculate Vmax and Km through both the initial rates and a time course analysis, allowing cross-validation of both methods. There are many additional interesting applications of this time course approach. For instance, the mode of action/mechanism of inhibitors can distinguished from time course rate profiles. This will be the topic of a future article.
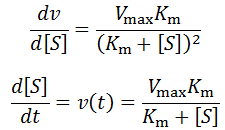
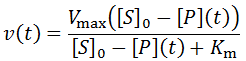
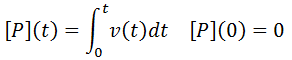
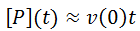
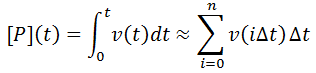
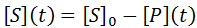
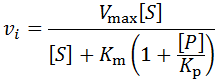
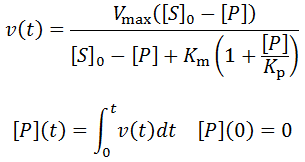
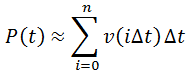
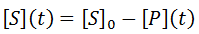
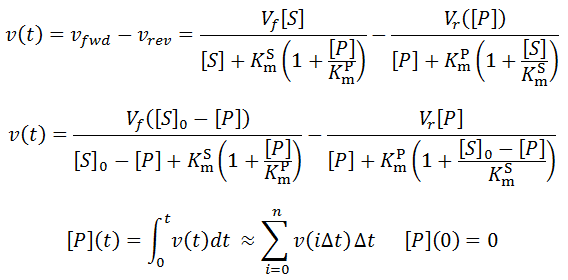
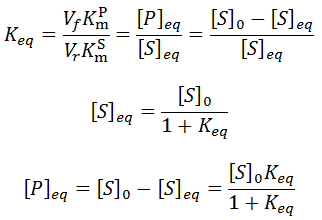
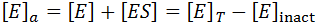
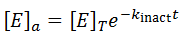
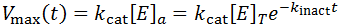
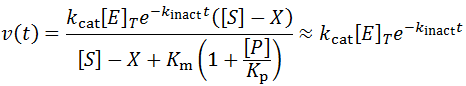
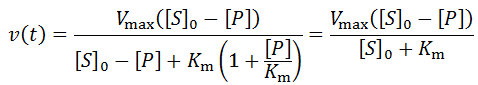
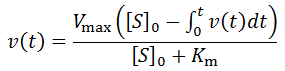
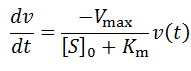
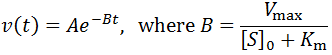
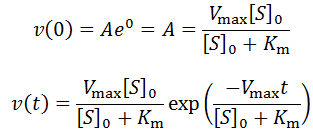
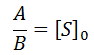
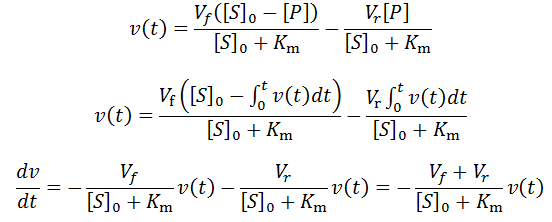
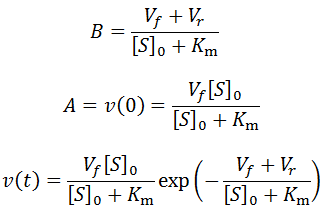
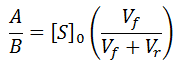
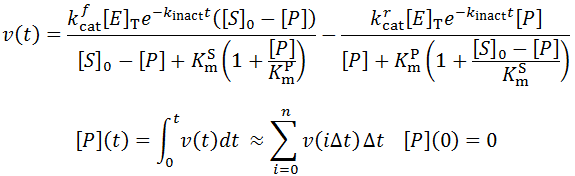
 RSS Feed
RSS Feed