G proteins are intracellular signaling molecules whose functions are governed by the GTPase cycle. An important class of G protein activators are guanine nucleotide exchange factors (GEFs), which catalyzes GDP-GTP exchange. The GEF mechanism is often considered irreversible. However, work by Stanley and Thomas using mathematical modelling showed that this assumption may lead to incorrect conclusions. In this article, I present simulations done by Stanley and Thomas. Furthermore, I extend this work, preforming simulations of an augmented model featuring a hypothetical GPCR-G protein signaling pathway. The expansion considers a multi-state GEF, an external ligand, and a multi-state G protein. Results from these simulations showed that G protein activation is controlled by a variety of factors including the concentration of GEF, the mode of GTPase activity, and internal protein dynamics.
Introduction
G proteins are a class of intracellular guanine nucleotide-binding proteins that play a role in signal transduction. Monomeric “small” G proteins control diverse cellular processes including proliferation, cell growth, apoptosis, membrane vesicle transport, cytoskeletal assembly, and protein synthesis [1]. In addition, the family of heterotrimeric G proteins (comprised of Gα, Gβ, and Gγ subunits) are involved in trans-membrane signaling through G protein-coupled receptors (GPCRs). They mediate changes in secondary messenger levels that underlie biological processes such as sensory perception, hormonal regulation, and immune responses.
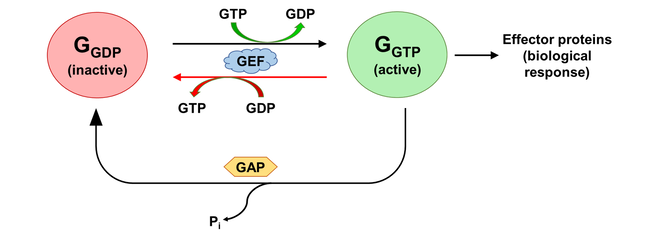
The activation states of a G protein are controlled by the GTPase cycle (Fig. 1). A G protein (GTPase) is considered “active” when bound to guanosine triphosphate (GTP). In this state, the G protein interacts with downstream effector proteins to elicit biological responses. Hydrolysis of GTP to guanosine diphosphate (GDP) deactivates the G protein, which can be re-activated by the exchange of GDP for GTP. The GTPase cycle may be regulated by accessory proteins. Deactivation is facilitated by GTPase activating proteins (GAPs), which couple to GTP-bound G proteins to stimulate their GTPase activity. On the other hand, activation is accelerated by the binding of guanine nucleotide exchange factors (GEFs), which catalyzes GDP/GTP exchange [2]. The mechanism of G protein-GEF interactions and the process of subsequent nucleotide exchange is of special interest to the field of GPCR signalling, where GPCRs fulfill the role of GEF and GTP hydrolysis occur through intrinsic GTPase activity of the heterotrimeric G proteins.
The activation states of a G protein are controlled by the GTPase cycle (Fig. 1). A G protein (GTPase) is considered “active” when bound to guanosine triphosphate (GTP). In this state, the G protein interacts with downstream effector proteins to elicit biological responses. Hydrolysis of GTP to guanosine diphosphate (GDP) deactivates the G protein, which can be re-activated by the exchange of GDP for GTP. The GTPase cycle may be regulated by accessory proteins. Deactivation is facilitated by GTPase activating proteins (GAPs), which couple to GTP-bound G proteins to stimulate their GTPase activity. On the other hand, activation is accelerated by the binding of guanine nucleotide exchange factors (GEFs), which catalyzes GDP/GTP exchange [2]. The mechanism of G protein-GEF interactions and the process of subsequent nucleotide exchange is of special interest to the field of GPCR signalling, where GPCRs fulfill the role of GEF and GTP hydrolysis occur through intrinsic GTPase activity of the heterotrimeric G proteins.
Figure 1. The activation state of a G protein is controlled by the GTPase cycle, where a G protein (GTPase) is inactive when bound to GDP and active when bound to GTP. The GTPase cycle is regulated by accessory proteins that mediate nucleotide exchange (GEF) and GTP hydrolysis (GAP). A reversible GEF mechanism is depicted, where read arrows indicate backward nucleotide exchange.
In addition to experimental and computational studies providing extensive structural and biochemical characterization [2-7], mathematical models have been developed for a number of G protein signaling pathways under various conditions [8-14]. Generally, the extent of activation is indicated by either an increase in concentration of an active G protein form (G-GTP in the case of small G proteins, Gα-GTP or Gβγ in the case of heterotrimeric G proteins), or a rise in downstream biological effect such as actin polymerization.
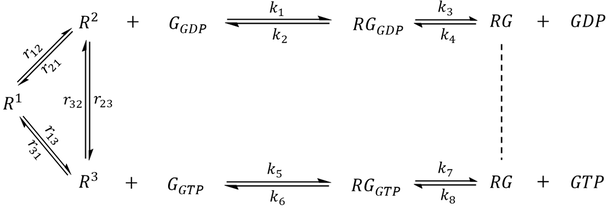
With few exceptions [12-13], GEF-catalyzed nucleotide exchange was considered irreversible. However, it was unclear whether the assumption holds under all circumstances. In their 2016 article, Stanley and Thomas investigated the effect of a reversible GEF mechanism on the behaviour of a small G protein regulatory system using mathematical modelling (Fig. 2) [13]. Their scheme contained a single GEF and a single G protein with either no GTPase activity, intrinsic GTPase activity, or GAP-mediated GTPase activity. The pathway is composed of reversible steps in which an irreversible GEF mechanism could be modelled by disallowing the dissociation of GTP from the GEF-G-GTP complex.
In addition to experimental and computational studies providing extensive structural and biochemical characterization [2-7], mathematical models have been developed for a number of G protein signaling pathways under various conditions [8-14]. Generally, the extent of activation is indicated by either an increase in concentration of an active G protein form (G-GTP in the case of small G proteins, Gα-GTP or Gβγ in the case of heterotrimeric G proteins), or a rise in downstream biological effect such as actin polymerization.
With few exceptions [12-13], GEF-catalyzed nucleotide exchange was considered irreversible. However, it was unclear whether the assumption holds under all circumstances. In their 2016 article, Stanley and Thomas investigated the effect of a reversible GEF mechanism on the behaviour of a small G protein regulatory system using mathematical modelling (Fig. 2) [13]. Their scheme contained a single GEF and a single G protein with either no GTPase activity, intrinsic GTPase activity, or GAP-mediated GTPase activity. The pathway is composed of reversible steps in which an irreversible GEF mechanism could be modelled by disallowing the dissociation of GTP from the GEF-G-GTP complex.
Figure 2. Schematic of a G protein-GEF interaction pathway adopted from Stanley and Thomas [13]. An irreversible GEF mechanism was modeled by assigning zero to the rate constant k7, which stops GTP release from the G-GTP-GEF complex (red arrow).
To remain physiologically relevant, kinetic parameters measured for the Ran:RCC1:RanGAP1 system were employed [15-16]. Ran (RAs-related nuclear protein, also known as GTP-binding nuclear protein) is a small 25 kDa G protein located preferentially in the cell nucleus. Together with regulatory proteins RCC1 (a GEF for Ran) and RanGAP1 (a GAP), it is involved in the transport of proteins and mRNAs across the nuclear membrane, as well as DNA synthesis and cell cycle progression [17]. Here, I replicate the simulations performed by Stanley and Thomas, and present an extension to their model. A hypothetical GPCR-G protein signaling pathway was constructed with consideration to functionally significant protein dynamics. The model was progressively augmented to include a multi-state GEF, a GPCR-activating ligand, and a multi-state G protein.
To remain physiologically relevant, kinetic parameters measured for the Ran:RCC1:RanGAP1 system were employed [15-16]. Ran (RAs-related nuclear protein, also known as GTP-binding nuclear protein) is a small 25 kDa G protein located preferentially in the cell nucleus. Together with regulatory proteins RCC1 (a GEF for Ran) and RanGAP1 (a GAP), it is involved in the transport of proteins and mRNAs across the nuclear membrane, as well as DNA synthesis and cell cycle progression [17]. Here, I replicate the simulations performed by Stanley and Thomas, and present an extension to their model. A hypothetical GPCR-G protein signaling pathway was constructed with consideration to functionally significant protein dynamics. The model was progressively augmented to include a multi-state GEF, a GPCR-activating ligand, and a multi-state G protein.
Mathematical models
Initial model
The initial model follows that from the article by Stanley and Thomas (Fig. 2). Six sets of simulations were performed comparing the three modes of GTPase activity (no GTPase, intrinsic GTPase, or GAP-mediated GTPase) paired with either a reversible or an irreversible GEF. The following list of ordinary differential equations (ODEs) were derived using the law of mass-action:
Here, GEF is represented by the variable E and the term f-GTPase accounts for changes in G-GXP as a result of GTP hydrolysis. In the absence of GTPase activity, f-GTPase = 0. For systems with intrinsic GTPase activity, f-GTPase = k-ase[G-GTP]. GAP-mediated GTPase reactions were modelled using Michaelis-Menten kinetics, which simplifies to:
where f0 is the total concentration of GAP. The model also assumes an excess of nucleotides and therefore constant values for [GDP] and [GTP]. Two additional equations relate to the conservation of mass of GEF and of G protein:
For each of the six conditions, two rounds of simulations were conducted. First, the model was simulated for 200 s to obtain the steady-state concentrations of each species in the pathway. These were used as initial conditions in a subsequent simulation lasting 30 s, where a 10-fold increase to the basal level of GEF was applied during the 10-20 s period. This provided insights into system behaviour as a function of GEF. All simulations were carried out using MATLAB’s built-in ODE solver ode15s suitable for stiff systems [18].
Extension 1: a multi-state GEF
In the following sections, an augmented model was implemented by considering a hypothetical GPCR-G protein system externally modulated by ligand binding. Experimentally, both GPCRs and G proteins exhibit slow-exchange dynamics and sample multiple conformational states on a μs to s timescale [5,6,19,20]. Motions at this timescale are associated with important biological functions such as docking, folding, and allosteric transitions.21 To explore this, a multi-state GPCR was introduced alongside a multi-state G protein engaging in state- and nucleotide-dependent interactions.
The first step of model extension replaced the generic GEF with a GPCR (R) that adopts three distinct conformational states- an inactive state R1 and two active-like states R2 and R3 capable of binding G protein (Scheme 1). Whereas R2 preferentially couples to G-GDP, the reversibility of GEF is preserved by R3, which preferentially couples to G-GTP. Since each state undergoes exchange with the other two, a receptor may sample all three conformations even in the absence of interacting partners.
The first step of model extension replaced the generic GEF with a GPCR (R) that adopts three distinct conformational states- an inactive state R1 and two active-like states R2 and R3 capable of binding G protein (Scheme 1). Whereas R2 preferentially couples to G-GDP, the reversibility of GEF is preserved by R3, which preferentially couples to G-GTP. Since each state undergoes exchange with the other two, a receptor may sample all three conformations even in the absence of interacting partners.
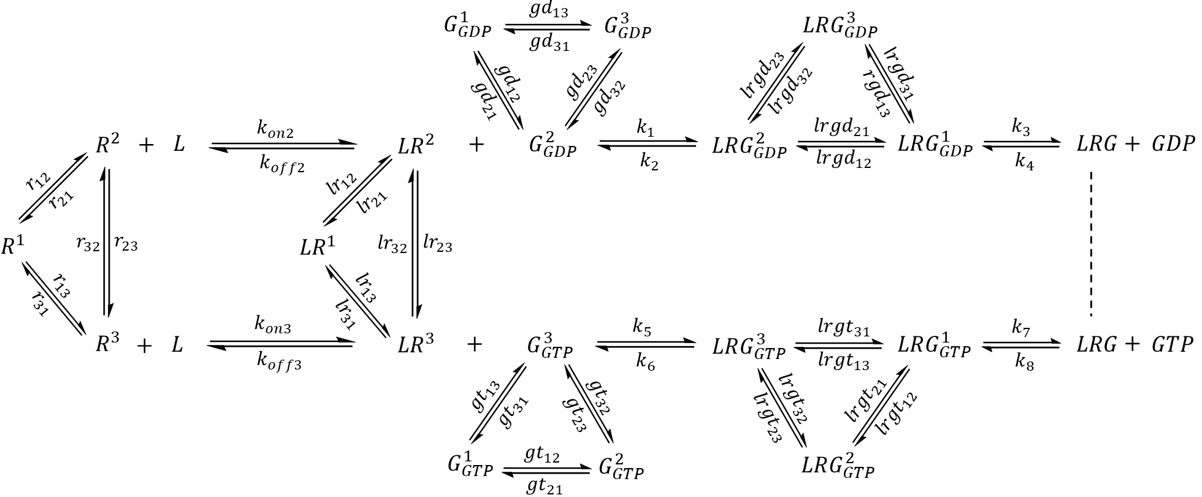
Scheme 1. A hypothetical GPCR-G protein signaling pathway. The receptor exhibits three major conformational states. R1 represents an inactive state while R2 and R3 are active states that preferentially bind to G-GDP and G-GTP, respectively.
The following set of ODEs were derived for Scheme 1 along with the conservation of mass of the receptor and the G protein:
The following set of ODEs were derived for Scheme 1 along with the conservation of mass of the receptor and the G protein:
For illustrative purposes, kinetic parameters from the initial model were used where applicable. The rate constants for the exchange between R1, R2, and R3 were chosen to be in the millisecond regime. In the absence of ligand and G protein, a population of receptors would show an equilibrium distribution of 69.0% R1, 17.2% R2, and 13.8% R3. Simulations were carried out assuming a reversible GEF and intrinsic GTPase activity. Like before, a first round of simulation provided steady-state concentrations, which were used as initial conditions in a subsequent 30 s simulation where a 10-fold increase in the total receptor concentration (R0) was introduced during the 10-20 s stimulation period.
Extension 2: introducing an agonist
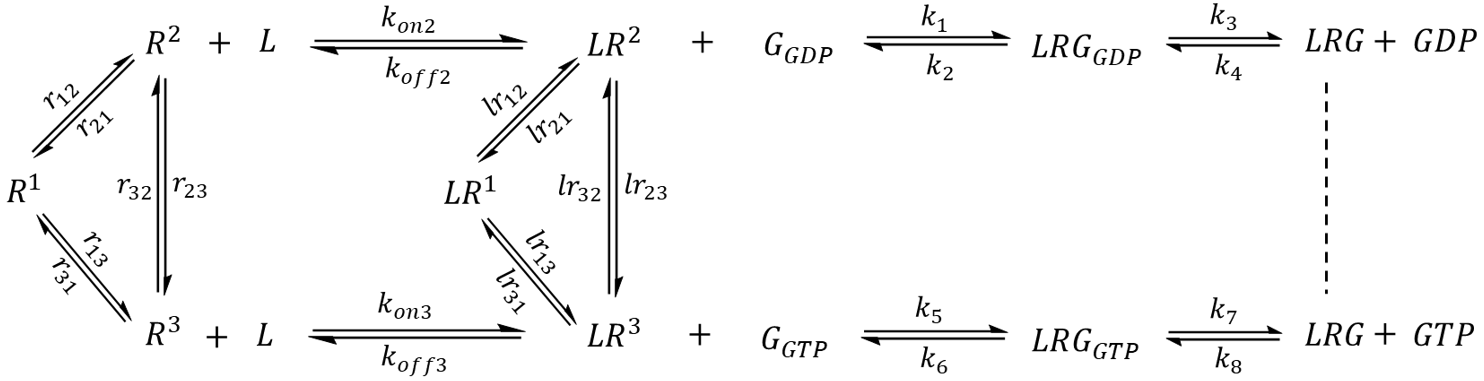
GPCR signaling is often regulated by an extracellular stimulus. In the second part of model extension, a receptor-activating ligand (an agonist) was introduced (Scheme 2). The ligand (L) binds to an active state of the receptor with medium-high affinity (Kd = 100 nM for R2 and Kd = 150 nM for R3) and an on rate (k-on) that is diffusion-limited (108 M-1 s-1) [22]. A receptor-ligand complex (LR) may sample all of the conformational states corresponding to that of an apo receptor, but has an altered equilibrium distribution that favors active-like conformations. The exchange rate constants (lr12, lr21, lr13, lr31, lr23, lr32) were chosen such that in the absence of external factors, a single LR complex will spend 11.8% of its time in the LR1 state, 58.8% of time as LR2, and 29.4% of time as LR3. Unlike the previous model, a G protein may only couple to receptor-agonist complexes but not to the apo receptors.
Scheme 2. Extended model featuring a ligand that binds to active-like states of the receptor and acts as a modulator to the G protein pathway. The model assumes that only ligand-bound receptors may couple to G protein.
The following ODEs were obtained for Scheme 2 along with the conservation of mass of the receptor, the G protein, and the ligand:
The following ODEs were obtained for Scheme 2 along with the conservation of mass of the receptor, the G protein, and the ligand:
Two rounds of simulations were performed. In the first round, a sub-stochiometric, 10:1 receptor-ligand ratio was employed to obtain steady-state concentrations at the end of 200 s. The model was then simulated from steady state for another 50 s, where the ligand concentration was elevated 10-fold (1:1 receptor-ligand ratio) from 10 s to 20 s and 100-fold (1:10 receptor-ligand ratio) from 30 s to 40 s.
Extension 3: a multi-state G protein
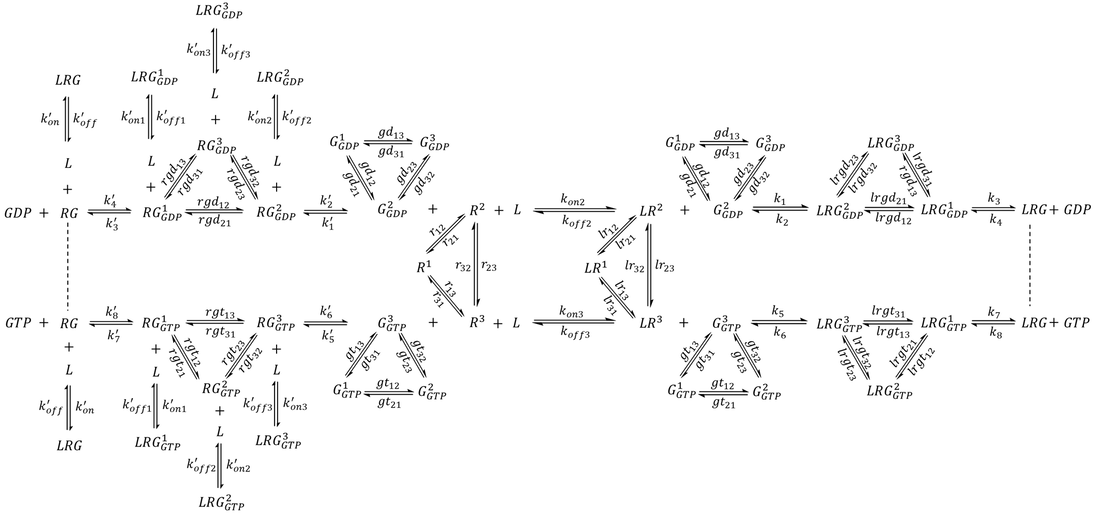
The Gα protein may adopt at least three distinct conformations-GDP-bound, GTP-bound, and a receptor-bound, nucleotide-free conformation [6,23]. In this section, the model was augmented further to incorporate a G protein that samples all three conformations whose populations and lifetimes are regulated by the binding of nucleotides as well as the receptor. The model is presented in Scheme 3. Here, G1 represents a G protein conformation with weaker affinity to nucleotides. G2 represents a G protein conformation that preferentially binds to GDP and LR2, while G3 is a conformation with higher affinity to GTP and LR3. The exchange rate constants were selected such that in the absence of external factors, a GDP-bound G protein will spend 4.8% of time as G1-GDP, 76.2% of time as G2-GDP, and 19.0% of time as G3-GDP. Similarly, a population of GTP-bound G protein will contain 3.2% G1-GTP, 16.1% G2-GTP, and 80.7% G3-GTP. For simplicity, the model contained only one species for the nucleotide-free LRG complex, which is known to be exceptionally stable and exhibit lifetimes of 5-10 min in the absence of nucleotides [7].
Scheme 3. Complete extended model featuring a three-state G protein. For simplicity, only one state was assigned to the nucleotide-free LRG complex.
An agonist-bound receptor may accelerate nucleotide exchange in the G protein via several processes. The receptor may facilitate nucleotide release by promoting LRG1-GDP, which has a reduced affinity to nucleotides. The binding of activated receptor stabilizes LRG, which assists in the complete dissociation of GDP and the diffusion of GTP to the nucleotide binding site. The subsequent binding of GTP (and to some extent re-association of GDP) significantly reduces receptor-G protein affinity, which helps to produce free active G proteins and regenerate receptors for another round of activation. While the latter two processes have both been observed experimentally [7,23], the conformational landscape of receptor-bound, multi-state G proteins have not yet been studied. To explore this model, the following list of ODEs were simulated:
An agonist-bound receptor may accelerate nucleotide exchange in the G protein via several processes. The receptor may facilitate nucleotide release by promoting LRG1-GDP, which has a reduced affinity to nucleotides. The binding of activated receptor stabilizes LRG, which assists in the complete dissociation of GDP and the diffusion of GTP to the nucleotide binding site. The subsequent binding of GTP (and to some extent re-association of GDP) significantly reduces receptor-G protein affinity, which helps to produce free active G proteins and regenerate receptors for another round of activation. While the latter two processes have both been observed experimentally [7,23], the conformational landscape of receptor-bound, multi-state G proteins have not yet been studied. To explore this model, the following list of ODEs were simulated:
Two rounds of simulations were carried out. In the first round, conditions were set up such that receptor binding would not alter the inherent G protein dynamics. In other words, the set of exchange rate constants experienced by the ligand-receptor-G protein complexes (lrgd12, lrgd21, lrgd13, lrgd31, lrgd23, lrgd32) were identical to the corresponding rate constants for the G protein alone (gd12, gd21, gd13, gd31, gd23, gd32). The steady state concentrations at the end of 200 s were used as initial conditions in a subsequent round of 120 s-long simulation, where rate constants were modified. Specifically, the value of lrgd21 was elevated 10-fold during the 20-50 s period, and the value of k6 was increased 10-fold during the 70-100 s period. The simulations were performed twice, for a system with intrinsic GTPase activity and for a system with hypothetical GAP-mediated GTPase activity.
Results and Discussion
GEF may serve versatile functions in a GTPase cycle
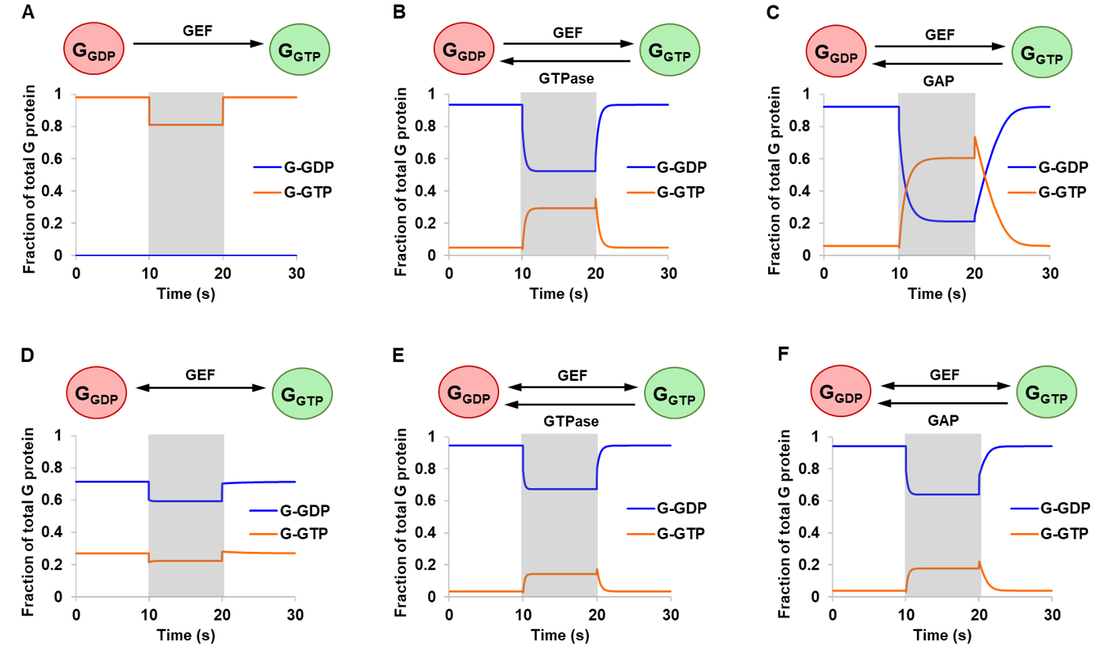
Results from the article by Stanley and Thomas were successfully replicated. Simulation results are presented in Fig. 3 monitoring free G-GDP and G-GTP as a fraction of total G protein. The extent of activation is represented by G-GTP, the active form of G protein. For systems with intrinsic (Fig. 3B and 3E) or GAP-mediated (Fig. 3C and 3F) GTPase activity, qualitatively similar outcomes were obtained for the reversible and the irreversible mechanism (ignoring differences in magnitude). In all four cases, a 10-fold amplification of GEF resulted in an increased level of G-GTP and a corresponding drop in G-GDP, consistent with the biological role of GEF in accelerating nucleotide exchange.
In the absence of GTPase activity, the reversible and the irreversible GEF mechanism showed qualitatively different system behaviour especially with respect to steady state concentrations (Fig. 3A and 3D). The addition of GEF triggered a drop in G-GTP, which can be attributed to its sequestration into GEF-G protein complexes. From these, Stanley and Thomas argued that 1) GEF can be stimulating as well as inhibitory and 2) the assumption of an irreversible model may lead to incorrect conclusions or predictions of system behaviour [13].
In the absence of GTPase activity, the reversible and the irreversible GEF mechanism showed qualitatively different system behaviour especially with respect to steady state concentrations (Fig. 3A and 3D). The addition of GEF triggered a drop in G-GTP, which can be attributed to its sequestration into GEF-G protein complexes. From these, Stanley and Thomas argued that 1) GEF can be stimulating as well as inhibitory and 2) the assumption of an irreversible model may lead to incorrect conclusions or predictions of system behaviour [13].
Figure 3. Simulations of the initial model. Starting at steady state concentrations, a stimulation of 10-fold increase in total GEF was applied at the start of 10 s and turned off at the end of 20 s (shaded regions). Six different conditions were simulated comparing an irreversible GEF mechanism (panels A-C) and a reversible GEF mechanism (panels D-F), with G protein exhibiting either no GTPase activity (panels A and D), intrinsic GTPase activity (panels B and E), or GAP-mediated GTPase activity (panels C and F). G-GXP denotes GXP-bound G protein.
System behaviour is a function of changing conformational landscapes
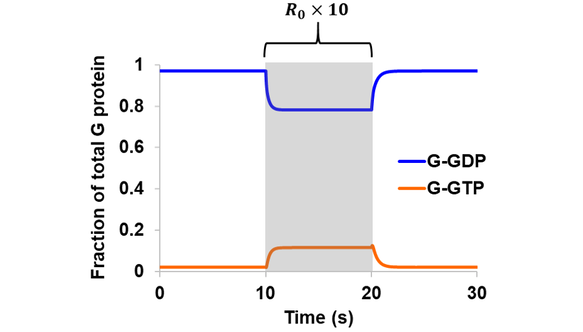
In the first extension to the original model, a three-state GEF (GPCR) was introduced and the same simulations were performed as above assuming a reversible GEF and intrinsic GTPase. Qualitatively similar results were obtained in comparison to the initial model, where a 10-fold increase in total receptor concentration led to a rise in G-GTP and a corresponding drop in G-GDP (Fig. 4). The magnitude of change is smaller in the case of the three-state GEF, since only a fraction of total receptors at a time could bind G-GDP to drive the cycle forward. For example, the level of G-GTP during R0 stimulation (at ~15 s) is 81.1% the value obtained from the original model featuring a one-state GEF.
Figure 4. Simulation of Scheme 1 assuming reversible GEF mechanism and intrinsic GTPase activity. The model (containing a three-state receptor) was simulated from steady state. A stimulation of 10-fold increase in total receptor concentration was introduced during the 10-20 s period (shaded region).
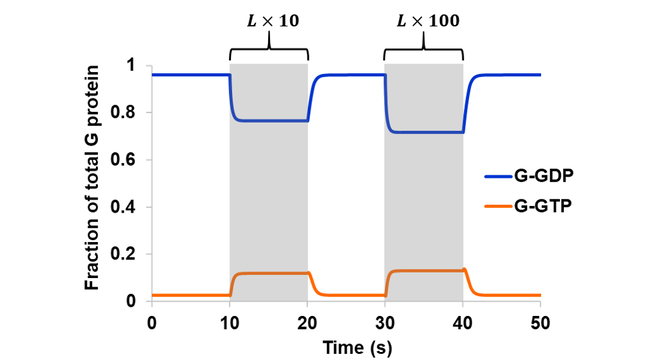
In the second part of model expansion, an external ligand was introduced. In literature, GPCR activation is often described in terms of structural changes in the receptor upon agonist binding, leading to an “active” conformation capable of coupling to G proteins [24]. From an ensemble perspective, however, a receptor samples all available conformations even in its apo form [20]. Perturbations in the environment leads to an altered energy landscape and a redistribution of states. Here, receptor activation is accomplished through an increase in the active-like conformations (LR2 and to some extent LR3) upon ligand binding, which led to an increased level of active G protein (Fig. 5). The degree of system response is a function of ligand concentration. Elevating the receptor-ligand ratio from sub-stoichiometric (10:1) to 1:1 resulted in a 4.5-fold increase in G-GTP. Another 10-fold increase in ligand (1:10 receptor-ligand ratio), approaching saturating concentration, only gave rise to an additional 1.1-fold increase in G-GTP.
In the second part of model expansion, an external ligand was introduced. In literature, GPCR activation is often described in terms of structural changes in the receptor upon agonist binding, leading to an “active” conformation capable of coupling to G proteins [24]. From an ensemble perspective, however, a receptor samples all available conformations even in its apo form [20]. Perturbations in the environment leads to an altered energy landscape and a redistribution of states. Here, receptor activation is accomplished through an increase in the active-like conformations (LR2 and to some extent LR3) upon ligand binding, which led to an increased level of active G protein (Fig. 5). The degree of system response is a function of ligand concentration. Elevating the receptor-ligand ratio from sub-stoichiometric (10:1) to 1:1 resulted in a 4.5-fold increase in G-GTP. Another 10-fold increase in ligand (1:10 receptor-ligand ratio), approaching saturating concentration, only gave rise to an additional 1.1-fold increase in G-GTP.
Figure 5. The model in Scheme 3 was simulated assuming a reversible GEF mechanism and intrinsic GTPase activity. Simulation began at steady state with a sub-stoichiometric (10:1) receptor-ligand ratio. The system was then stimulated with a 10-fold increase in ligand during the 10-20 s period, and a 100-fold increase in ligand during the 30-40 s period (shaded regions).
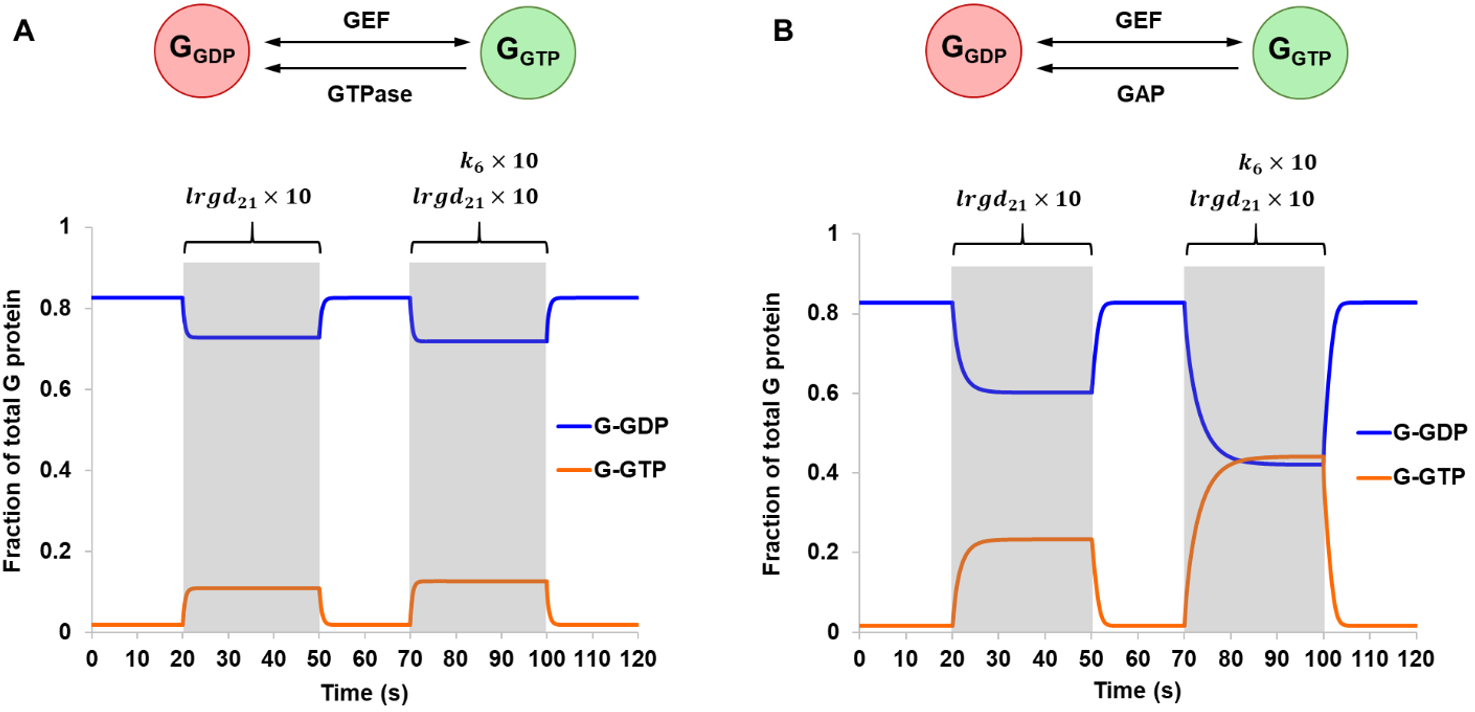
Lastly, a multi-state G protein was considered. In this model, a G protein may sample three major conformational states whose populations and lifetimes are modulated by binding partners such the nucleotides and the agonist-bound receptor. The simulation explored two different methods that a receptor may utilize to catalyze nucleotide exchange (Fig. 6). A receptor may influence the conformational landscape of a G protein to promote LRG1-GDP, a conformation with weaker affinity to nucleotides. Conceptually, this would facilitate GDP release and was reflected in the model by assigning a larger value to the rate constant lrgd21 (Scheme 3). As expected, a 5.8-fold increase in G-GTP was observed during the stimulation period when GTP hydrolysis occurred through intrinsic GTPase, and a 13.9-fold increase was observed in the case of a GAP-mediated GTPase. The system was further activated by increasing k6, the rate constant for the dissociation of G-GTP from LRG-GTP (Fig. 6). This is another step where the receptor may help to drive nucleotide exchange. Here, the effect of activation was much larger for a GAP-mediated GTPase in comparison to an intrinsic GTPase. These results point to the interdependency of different modes of pathway regulation and how they could be utilized in conjunction to control signal amplification levels.
Lastly, a multi-state G protein was considered. In this model, a G protein may sample three major conformational states whose populations and lifetimes are modulated by binding partners such the nucleotides and the agonist-bound receptor. The simulation explored two different methods that a receptor may utilize to catalyze nucleotide exchange (Fig. 6). A receptor may influence the conformational landscape of a G protein to promote LRG1-GDP, a conformation with weaker affinity to nucleotides. Conceptually, this would facilitate GDP release and was reflected in the model by assigning a larger value to the rate constant lrgd21 (Scheme 3). As expected, a 5.8-fold increase in G-GTP was observed during the stimulation period when GTP hydrolysis occurred through intrinsic GTPase, and a 13.9-fold increase was observed in the case of a GAP-mediated GTPase. The system was further activated by increasing k6, the rate constant for the dissociation of G-GTP from LRG-GTP (Fig. 6). This is another step where the receptor may help to drive nucleotide exchange. Here, the effect of activation was much larger for a GAP-mediated GTPase in comparison to an intrinsic GTPase. These results point to the interdependency of different modes of pathway regulation and how they could be utilized in conjunction to control signal amplification levels.
Figure 6. Simulations of Scheme 3 comparing an intrinsic GTPase (A) and a hypothetical GAP-mediated GTPase (B), both assuming reversible GEF mechanism. The model was simulated from steady-state and stimulation was applied at two different time points. From 20 s to 50 s, a 10-fold increase in the rate constant lrgd21 was introduced. This was repeated from 70 s to 100 s but with the addition of a 10-fold increase in the rate constant k6.
Conclusion and Future Work
This article presented a step-by-step expansion to the model proposed by Stanley and Thomas describing a G protein signaling pathway. Results from the original article were replicated and demonstrated qualitatively different system behaviour between a reversible and an irreversible GEF mechanism. From this point, three new elements were introduced: a multi-state GEF in the form of a GPCR, a multi-state G protein, and an external ligand in the form of an agonist. The augmented model showed qualitatively similar response (increased levels of G-GTP) to activating stimuli. Differences in magnitude can be attributed to the addition of new variables and steps in the pathway. The results demonstrated the importance of considering functionally significant conformational states in model building and point to the utility of protein dynamics as a tool to regulate biological pathways. The current model is nonetheless a simplification in comparison to a real biological system. It described a minimal G protein system that is homogeneous in space with no external influences or localization effects. The model could be improved by incorporating precoupling, a process where the coupling of receptor and G protein occurs prior to or in the absence of agonist binding (Scheme 4). Additional variables such as Gβγ, downstream effector proteins, or allosteric regulators may also be included.
Scheme 4. Schematic of a multi-state GPCR-G protein pathway incorporating precoupling processes.
Author’s note: the MATLAB codes used, simulation parameters, and data presented in this article are available upon request. This article was originally written in 2017 and has not been updated to consider more recent literature.
Author’s note: the MATLAB codes used, simulation parameters, and data presented in this article are available upon request. This article was originally written in 2017 and has not been updated to consider more recent literature.
References
[1] Csépányi-Kömi, R., Lévay, M. & Ligeti, E. Small G proteins and their regulators in cellular signalling. Mol. Cell. Endocrinol. 353, 10–20 (2012).
[2] Bos, J. L., Rehmann, H. & Wittinghofer, A. GEFs and GAPs: Critical Elements in the Control of Small G Proteins. Cell 129, 865–877 (2007).
[3] Sprang, S. R. Invited review: Activation of G proteins by GTP and the mechanism of Gα-catalyzed GTP hydrolysis. Biopolymers 105, 449–462 (2016).
[4] Vetter, I. R. & Wittinghofer, A. The Guanine Nucleotide-Binding Switch in Three Dimensions. Science. 294, 1299–1304 (2001).
[5] Dror, R. O. et al. Structural Basis for Nucleotide Exchange in Heterotrimeric G Proteins. Science. 348, 1361–1365 (2015).
[6] Goricanec, D. et al. Conformational dynamics of a G-protein α subunit is tightly regulated by nucleotide binding. Proc. Natl. Acad. Sci. 113, E3629–E3638 (2016).
[7] Gregorio, G. G. et al. Single-molecule analysis of ligand efficacy in β2AR-G-protein activation. Nature 547, 68–73 (2017).
[8] Khatibi, S., Rios, K. I. & Nguyen, L. K. in Methods in molecular biology (ed. Rivero, F.) 3–20 (Springer New York, 2018). doi:10.1007/978-1-4939-8612-5_1
[9] Yi, T.-M., Kitano, H. & Simon, M. I. A quantitative characterization of the yeast heterotrimeric G protein cycle. Proc. Natl. Acad. Sci. 100, 10764–10769 (2003).
[10] Hao, N., Yildirim, N., Wang, Y., Elston, T. C. & Dohlman, H. G. Regulators of G protein signaling and transient activation of signaling: Experimental and computational analysis reveals negative and positive feedback controls on G protein activity. J. Biol. Chem. 278, 46506–46515 (2003).
[11] Adams, J. A., Omann, G. M. & Linderman, J. J. A mathematical model for ligand/receptor/G-protein dynamics and actin polymerization in human neutrophils. J. Theor. Biol. 193, 543–560 (1998).
[12] Bornheimer, S. J., Maurya, M. R., Farquhar, M. G. & Subramaniam, S. Computational modeling reveals how interplay between components of a GTPase-cycle module regulates signal transduction. Proc. Natl. Acad. Sci. U. S. A. 101, 15899–15904 (2004).
[13] Stanley, R. J. & Thomas, G. M. H. Activation of G Proteins by Guanine Nucleotide Exchange Factors Relies on GTPase Activity. PLoS One 11, e0151861 (2016).
[14] Bridge, L. J., Mead, J., Frattini, E., Winfield, I. & Ladds, G. Modelling and simulation of biased agonism dynamics at a G protein-coupled receptor. J. Theor. Biol. 442, 44–65 (2018).
[15] Klebe, C., Wittinghofer, A., Bischoff, F. R. & Ponstingl, H. Interaction of the Nuclear GTP-Binding Protein Ran with Its Regulatory Proteins RCC1 and RanGAP1. Biochemistry 34, 639–647 (1995).
[16] Klebe, C., Prinz, H., Wittinghofer, A. & Goody, R. S. The Kinetic Mechanism of Ran-Nucleotide Exchange Catalyzed by RCC1. Biochemistry 34, 12543–12552 (1995).
[17] Hadjebi, O., Casas-Terradellas, E., Garcia-Gonzalo, F. R. & Rosa, J. L. The RCC1 superfamily: From genes, to function, to disease. Biochim. Biophys. Acta - Mol. Cell Res. 1783, 1467–1479 (2008).
[18] MATLAB. 9.5 (R2018b). Mathworks Inc. Natick, MA (2018).
[19] Lohse, M. J. et al. Kinetics of G-protein-coupled receptor signals in intact cells. Br. J. Pharmacol. 153, 125–132 (2008).
[20] Ye, L., Van Eps, N., Zimmer, M., Ernst, O. P. & Prosser, R. S. Activation of the A2A adenosine G-protein-coupled receptor by conformational selection. Nature 533, 265–268 (2016).
[21] Teilum, K., Olsen, J. G. & Kragelund, B. B. Functional aspects of protein flexibility. Cell. Mol. Life Sci. 66, 2231–2247 (2009).
[22] Lane, J. R., May, L. T., Parton, R. G., Sexton, P. M. & Christopoulos, A. A kinetic view of GPCR allostery and biased agonism. Nat. Chem. Biol. 13, 929–937 (2017).
[23] Rasmussen, S. G. F. et al. Crystal structure of the β¬2 adrenergic receptor – Gs protein complex. Nature 477, 549–555 (2011).
[24] Manglik, A. & Kruse, A. C. Structural Basis for G Protein-Coupled Receptor Activation. Biochemistry 56, 5628–5634 (2017).
[2] Bos, J. L., Rehmann, H. & Wittinghofer, A. GEFs and GAPs: Critical Elements in the Control of Small G Proteins. Cell 129, 865–877 (2007).
[3] Sprang, S. R. Invited review: Activation of G proteins by GTP and the mechanism of Gα-catalyzed GTP hydrolysis. Biopolymers 105, 449–462 (2016).
[4] Vetter, I. R. & Wittinghofer, A. The Guanine Nucleotide-Binding Switch in Three Dimensions. Science. 294, 1299–1304 (2001).
[5] Dror, R. O. et al. Structural Basis for Nucleotide Exchange in Heterotrimeric G Proteins. Science. 348, 1361–1365 (2015).
[6] Goricanec, D. et al. Conformational dynamics of a G-protein α subunit is tightly regulated by nucleotide binding. Proc. Natl. Acad. Sci. 113, E3629–E3638 (2016).
[7] Gregorio, G. G. et al. Single-molecule analysis of ligand efficacy in β2AR-G-protein activation. Nature 547, 68–73 (2017).
[8] Khatibi, S., Rios, K. I. & Nguyen, L. K. in Methods in molecular biology (ed. Rivero, F.) 3–20 (Springer New York, 2018). doi:10.1007/978-1-4939-8612-5_1
[9] Yi, T.-M., Kitano, H. & Simon, M. I. A quantitative characterization of the yeast heterotrimeric G protein cycle. Proc. Natl. Acad. Sci. 100, 10764–10769 (2003).
[10] Hao, N., Yildirim, N., Wang, Y., Elston, T. C. & Dohlman, H. G. Regulators of G protein signaling and transient activation of signaling: Experimental and computational analysis reveals negative and positive feedback controls on G protein activity. J. Biol. Chem. 278, 46506–46515 (2003).
[11] Adams, J. A., Omann, G. M. & Linderman, J. J. A mathematical model for ligand/receptor/G-protein dynamics and actin polymerization in human neutrophils. J. Theor. Biol. 193, 543–560 (1998).
[12] Bornheimer, S. J., Maurya, M. R., Farquhar, M. G. & Subramaniam, S. Computational modeling reveals how interplay between components of a GTPase-cycle module regulates signal transduction. Proc. Natl. Acad. Sci. U. S. A. 101, 15899–15904 (2004).
[13] Stanley, R. J. & Thomas, G. M. H. Activation of G Proteins by Guanine Nucleotide Exchange Factors Relies on GTPase Activity. PLoS One 11, e0151861 (2016).
[14] Bridge, L. J., Mead, J., Frattini, E., Winfield, I. & Ladds, G. Modelling and simulation of biased agonism dynamics at a G protein-coupled receptor. J. Theor. Biol. 442, 44–65 (2018).
[15] Klebe, C., Wittinghofer, A., Bischoff, F. R. & Ponstingl, H. Interaction of the Nuclear GTP-Binding Protein Ran with Its Regulatory Proteins RCC1 and RanGAP1. Biochemistry 34, 639–647 (1995).
[16] Klebe, C., Prinz, H., Wittinghofer, A. & Goody, R. S. The Kinetic Mechanism of Ran-Nucleotide Exchange Catalyzed by RCC1. Biochemistry 34, 12543–12552 (1995).
[17] Hadjebi, O., Casas-Terradellas, E., Garcia-Gonzalo, F. R. & Rosa, J. L. The RCC1 superfamily: From genes, to function, to disease. Biochim. Biophys. Acta - Mol. Cell Res. 1783, 1467–1479 (2008).
[18] MATLAB. 9.5 (R2018b). Mathworks Inc. Natick, MA (2018).
[19] Lohse, M. J. et al. Kinetics of G-protein-coupled receptor signals in intact cells. Br. J. Pharmacol. 153, 125–132 (2008).
[20] Ye, L., Van Eps, N., Zimmer, M., Ernst, O. P. & Prosser, R. S. Activation of the A2A adenosine G-protein-coupled receptor by conformational selection. Nature 533, 265–268 (2016).
[21] Teilum, K., Olsen, J. G. & Kragelund, B. B. Functional aspects of protein flexibility. Cell. Mol. Life Sci. 66, 2231–2247 (2009).
[22] Lane, J. R., May, L. T., Parton, R. G., Sexton, P. M. & Christopoulos, A. A kinetic view of GPCR allostery and biased agonism. Nat. Chem. Biol. 13, 929–937 (2017).
[23] Rasmussen, S. G. F. et al. Crystal structure of the β¬2 adrenergic receptor – Gs protein complex. Nature 477, 549–555 (2011).
[24] Manglik, A. & Kruse, A. C. Structural Basis for G Protein-Coupled Receptor Activation. Biochemistry 56, 5628–5634 (2017).
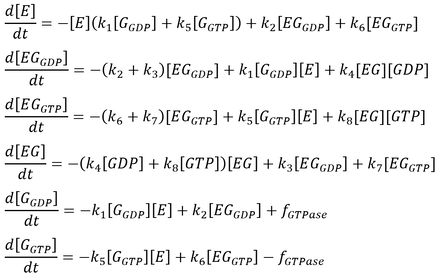
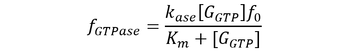
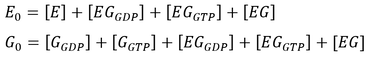
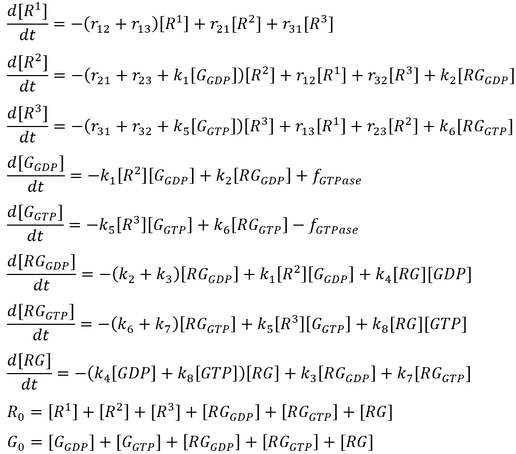


 RSS Feed
RSS Feed