Avogadro’s limit
How to dilute a solution to Avogadro’s limit
First, we must estimate the mass of a grain of salt. An average grain of regular table salt has dimensions of roughly 0.3 mm × 0.3 mm × 0.3 mm [1]. This corresponds to a volume of 2.7 × 10^-5 mL. The density of NaCl is 2.16 g/mL and so the grain contains roughly 5.83 x 10^-5 g. The molecular weight of NaCl is 58.44 g/mol, giving 9.98 × 10^-7 moles (n). Now we calculate what volume (V) we’d have to dissolve the salt grain in to reach Avogadro’s limit concentration (C).
Reaching Avogadro’s limit by serial dilution
Suppose we instead dilute our initial 1 L salt grain solution by adding 100 mL of it into a fresh 900 mL of water. Each dilution now achieves a 10-fold dilution factor.
Avogadro’s limit in homeopathy
The principles of homeopathy hopefully surprise and confuse you, as it goes against our most basic understanding of physics, chemistry and biology. All scientifically understood drugs exert their effects through physical or chemical interactions with the biological system. Surely a drug cannot interact with/modulate a biological system if none is administered. The most commonly proposed mechanism for homeopathy is the concept of “water memory,” that water molecules are permanently imprinted with the memory of compounds they’ve previously interacted with. Proponents even claim that this information is transmitted to new water molecules upon dilution. Of course, there are serious problems with these ideas. The structural features of water have been heavily studied and are well understood. Water molecules dynamically associate in a hydrogen-bonding network. Presumably, it is through this that the water could “remember.” Unfortunately for homeopathy though, it seems that water is rather forgetful. Experimentally, this network’s has been shown to be remarkably short-lived with all memory gone after only 50 femtoseconds [4].
The concept of water memory does not even require a scientific rebuttal to expose its absurdity, however. If water is imprinted with all chemicals it has ever meet, then just about all water on Earth would already have memory of near every conceivable medicine or toxin. Furthermore, recall the central premise that potency increases with dilution. It follows that the addition and subsequent dilution of a specific medicine would be ineffective at developing that particular activity over all others already present.
The probability of finding a molecule below Avogadro’s limit
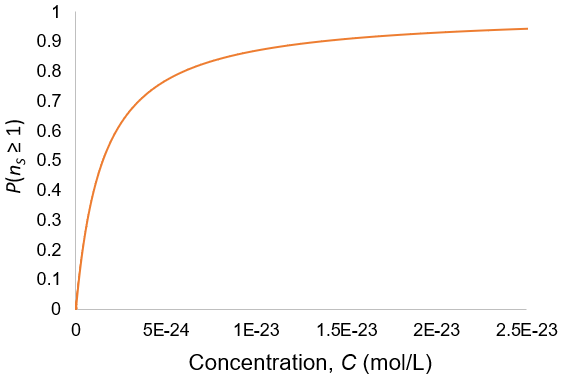
An interesting aspect of Avogadro’s limit is that here the law of large numbers no longer applies. Calculations of moles or concentrations near or below Avogadro’s limit must consider probability. Under these conditions, finding a molecule of interest in a given volume of a solution is probabilistic. Not only this, there is even uncertainty in the concentration of a prepared solution, as long as it is made by serial dilution. I am unaware of any attempts to account for the probabilistic nature of this situation, and so I conclude this article by developing a numerical solution below.
Suppose we have a solution of a molecule of interest at concentration C with volume VT. We withdraw a sample of volume VS. What is the probability of the sample containing nS molecules?
Broadly, the probability of an event is given by the ratio of how many ways there are for the desired outcome to occur over the total number of possible outcomes. We can calculate the probability of the stated event by developing expressions for these two quantities. In doing so, it is helpful to divide the total solution into imaginary Vs-sized portions, with the molecules randomly distributed among them.
We can evaluate the total number of possible outcomes from our random sample by noticing that this is equivalent to a classic combinatorics problem: sorting x identical objects into r distinct groups. The number of possible outcomes is given by the following combination [5]:
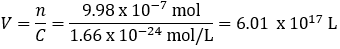
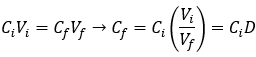
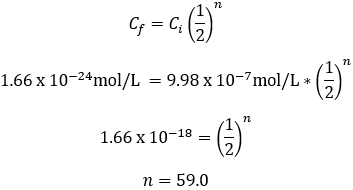
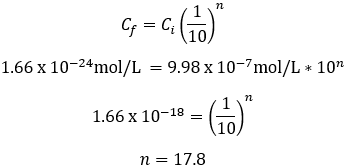
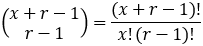
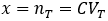
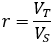
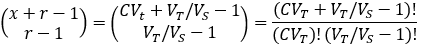
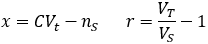
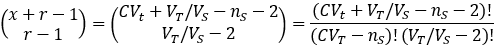
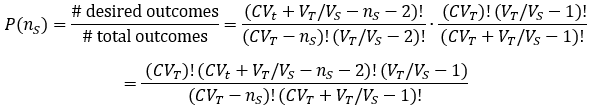
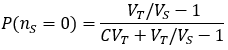
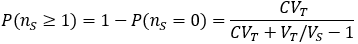
 RSS Feed
RSS Feed