In enzymology, inhibitors are categorized by their kinetic mechanism. In this article, I examine and clarify differences between a few common reversible inhibition mechanisms: competitive, uncompetitive, non-competitive, and mixed. Overall, these differ in which step(s) in the catalytic cycle are perturbed by the inhibitor. Based on this, differences between their inhibition kinetics can be rationalized.
Competitive inhibition
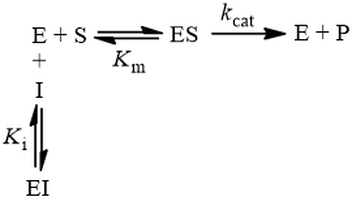
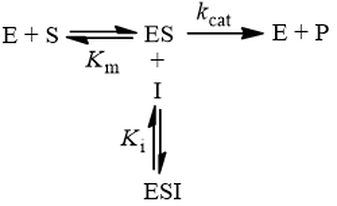
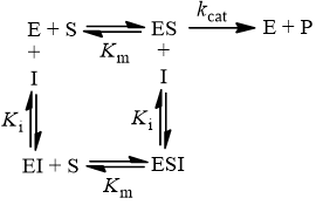
In competitive inhibition, the inhibitor (I) binds only to free enzyme (E), not to the enzyme-substrate complex (ES):
This mechanism is called competitive because the inhibitor “competes” with substrate for binding the active site of the enzyme. By reducing the availability of this site for substrate binding, product formation is hindered. Kinetically, competitive inhibitors are characterised by the following initial velocity equation:
Where vi is the initial velocity, Vmax is the maximum velocity (the product of kcat and total enzyme concentration), [S] is the substrate concentration, Km is the Michaelis constant, [I] is the inhibitor concentration, and Ki is the inhibition constant. To understand the kinetics of this inhibition mechanism more clearly, we can put this in the simplified form of the Michaelis-Menten equation:
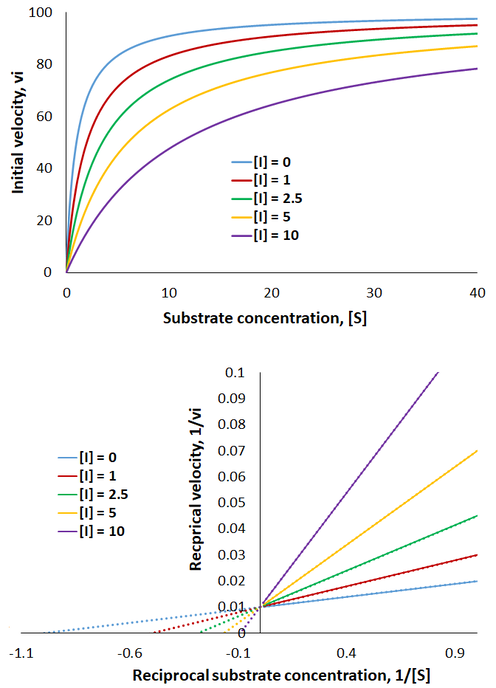
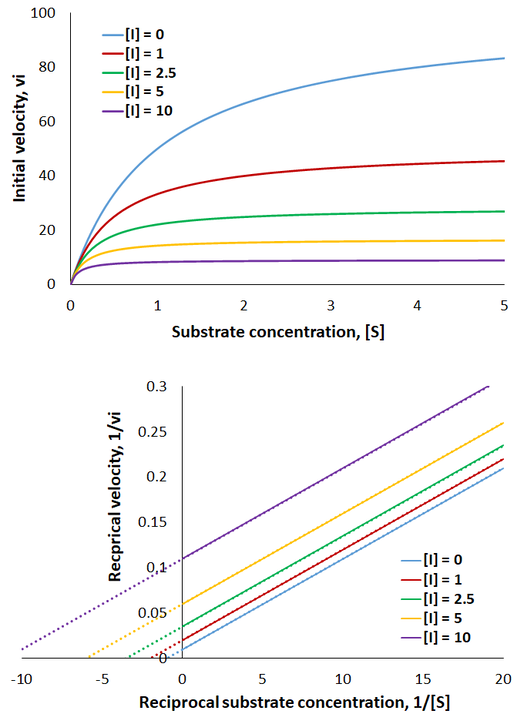
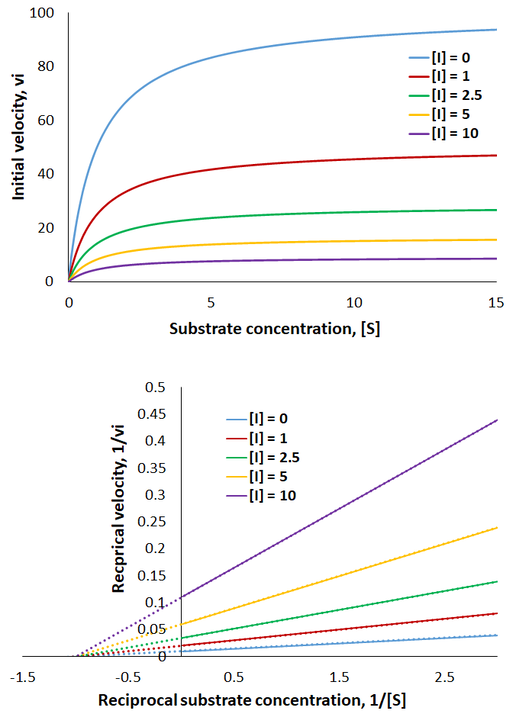
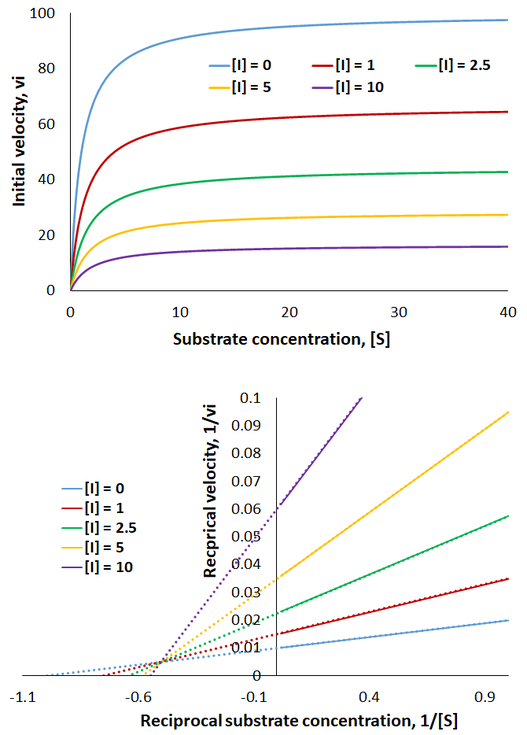
Therefore, the presence of competitive inhibitor increases the “apparent” Km value (Km app). This value refers to the substrate concentration required to achieve half maximum reaction velocity. Because the inhibitor is competing for active site binding, more substrate is required to overcome this and achieve enzyme saturation. Important in comparison to other inhibition mechanisms, competitive inhibitors have no effect on Vmax (the maximum reaction rate). To visualize competitive inhibition kinetics, I plot Michaelis-Menten curves and a Lineweaver-Burk plot under increasing amounts of inhibitor:
The presence of competitive inhibitor necessitates higher substrate concentrations to reach enzyme saturation. However, the rate still plateaus at the same maximum level as the uninhibited reaction. Thus, in the Lineweaver-Burk plot the magnitude of the x-intercepts decrease (apparent Km increases) while the y-intercepts are constant (Vmax is unchanged).
Uncompetitive inhibition
In uncompetitive inhibition, the inhibitor binds only to the enzyme-substrate complex:
This mechanism is called “uncompetitive” in contrast to competitive inhibition. While competitive inhibition can be overcome at high substrate concentrations, uncompetitive inhibition cannot. Instead, uncompetitive inhibitors sequester enzyme-substrate complex into a catalytically inactive ESI ternary complex. The initial velocity equation of this inhibition type is:
Putting this in the form of the Michaelis-Menten equation:
Therefore, the inhibitor decreases both the Km and Vmax values by the same factor relative to the uninhibited reaction. That is, less substrate is required to reach the maximum enzyme rate, but that maximum rate is reduced. It is an important and diagnostic feature of this mechanism that apparent Km and Vmax are decreased by the same amount, meaning that the apparent Vmax/Km ratio is unchanged. To demonstrate uncompetitive inhibition kinetics, here are Michaelis-Menten curves and a Lineweaver-Burk plot at several inhibitor concentrations:
Uncompetitive inhibition decreases the maximum reaction rate, but also makes enzyme saturation occur more readily at lower substrate concentrations. This has an interesting consequence: uncompetitive inhibition is most effective under substrate-saturating conditions. In fact, at very low substrate concentrations there is minimum inhibition. Because this inhibitor class decreases apparent Vmax and Km by the same fold, the catalytic efficiency of the enzyme is unchanged. At low substrate concentrations below Km, the observed rate approximates the enzyme’s catalytic efficiency, accounting for the lack of inhibition under these conditions. In the Lineweaver-Burk plot, a series of parallel lines is obtained because the slope equals Km/Vmax.
Non-competitive inhibition
In non-competitive inhibition the inhibitor binds to both free enzyme (E) and enzyme substrate complex (ES) with equal affinity:
Non-competitive inhibition cannot be overcome by high substrate concentrations, accounting for the name. Like the uncompetitive mechanism, non-competitive inhibition reduces substrate turnover through formation of a catalytically inactive ESI complex. However, this mechanism is distinct from uncompetitive inhibition in that the inhibitor can also bind to free enzyme. Admittingly, it is particularly easy to mix up non-competitive and uncompetitive inhibition since both “un” and “non” prefixes are synonyms in regular English. Non-competitive inhibition follows this initial velocity equation:
Putting this in the form of the Michaelis-Menten equation:
Non-competitive inhibition has no effect on substrate binding, as Km is unchanged. This inhibitor type exclusively decreases Vmax. To further explore non-competitive inhibition kinetics, I plot Michaelis-Menten curves and a Lineweaver-Burk plot over a range of inhibitor concentrations:
Non-competitive inhibition decreases the maximum reaction rate, while having no effect on how quickly substrate saturation is achieved. While competitive and uncompetitive inhibition works best at low or high substrate concentrations respectively, non-competitive inhibition is unaffected by it. The percent inhibition is constant over the full range of substrate concentrations, a consequence of Vmax being decreased while Km is unperturbed. Therefore, in the Lineweaver-Burk plot the y-intercepts decrease with increasing levels of inhibitor, while the x-intercepts are constant.
Mixed inhibition
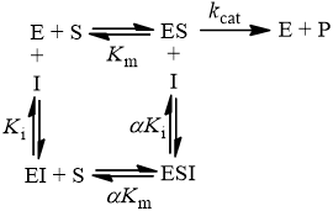
Mixed inhibition involves inhibitor binding to both free enzyme and enzyme-substrate complex with different binding constants (Ki and αKi):
Mixed inhibition is a general model that all previously mentioned mechanisms are special cases of. It can be thought of a blend between competitive and uncompetitive modes, weighted by the relative values of Ki and αKi. Furthermore, in the special case where α = 1, the inhibitor’s binding affinity for free enzyme (E) and enzyme-substrate complex (ES) are equal and the scheme simplifies to non-competitive inhibition. Its initial velocity equation is:
Putting this in the form of the Michaelis-Menten equation:
Mixed inhibitors have the most complex kinetics modifying apparent Km, Vmax and Vmax/Km values, the relative effects on each depend on the sizes of the Ki and αKi values. To further explore this, I plot Michaelis-Menten curves and a Lineweaver-Burk plot under increasing amounts of mixed inhibitor:
It is challenging to generalize about the appearance of mixed inhibition, since it depends on the relative values of Ki and αKi. Both the maximum reaction rate and the amount of substrate required for enzyme saturation change, but not by the same amount. The Lineweaver-Burk plot is characterized by changing x- and y-intercepts with the lines crossing between the x- and y- axes. This is a consequence of Vmax, Km, and their ratio each being modified.
How to differentiate the inhibition mechanisms
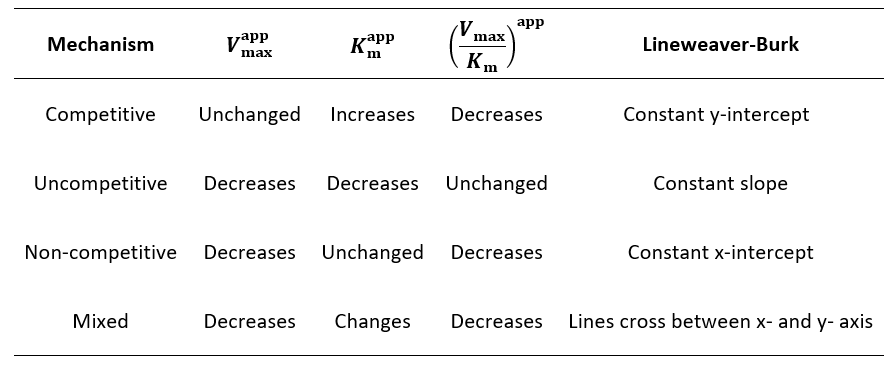
To conclude, I summarize the differences between these reversible enzyme inhibitor types in the table below. Each inhibition mechanism has a unique pattern of effects on the kinetic parameters Vmax (the maximum reaction rate), Km (how much substrate it takes to reach saturation) and Vmax/Km (a measure of catalytic efficiency). Thus, by analyzing an inhibitor’s action in a series of Michaelis-Menten curves or a Lineweaver-Burk plot, the mechanism can be quickly identified.
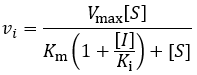
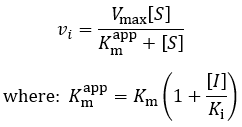
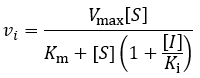
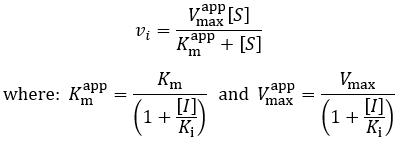
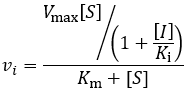
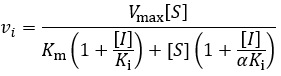
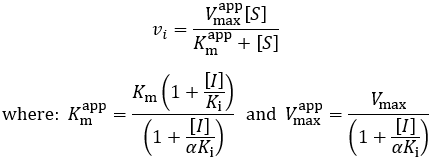
 RSS Feed
RSS Feed