Temperature (T) has a specific definition. The inverse of temperature is the change in entropy (S) that results from a small change in internal energy (U) for a system with constant volume (V) and number of molecules (N).
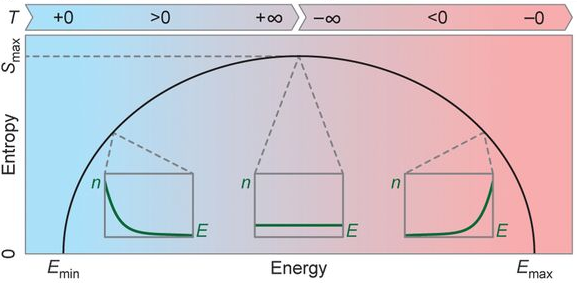
Entropy measures disorder, the number of possible microscopic arrangements which would produce the macroscopically observed properties. Increasing the internal energy of a system usually increases its entropy (for positive temperatures). This makes sense because a system which has more energy will be more likely to occupy high energy states, resulting in a larger number of possible microscopic states and hence more disorder. Maximum entropy is achieved in the extreme case where the system is equally likely to be in every energy state that it is allowed to occupy. However, most systems do not have an upper bound on the allowed energy states, only a lower bound. If an infinite number of energy states are allowed, then the system’s entropy can increase without restraint. Systems with both upper and lower bounds on the allowed energies, conversely, have a maximum entropy that they can obtain. This will become important later because it is a necessary condition a system must satisfy to have negative absolute temperature. Since dS=0 at the maximum, it occurs only at temperatures of infinity or negative infinity. Notice that
A system has an absolute negative temperature when it contains more internal energy than at the point where maximum entropy is obtained (at a temperature of infinity or negative infinity). This shows why the existence of such temperatures does not violate the third law of thermodynamics. If we increase the internal energy at a temperature of positive infinity it jumps directly to negative kelvins, skipping absolute zero. It now should also be clear why a system must have both upper and lower bounds on its allowed energy states to reach negative absolute temperature. If this condition was not met then maximum entropy would occur at infinite internal energy. In order to have more internal energy than this we would require it to be greater than infinity which obviously is absurd.
We can understand negative absolute temperatures more meaningfully by thinking about how they affect the distribution of energy states the system has. The probability that a system is in a particular energy state is given by something called the Boltzmann factor. It says that the probability of the system being in a particular energy state is proportional to negative exponential of the energy of the state divided by the Boltzmann constant (K) and the temperature.
Much of what I have discussed here is quite abstract. You might be wondering how you would actually go about reaching negative temperatures. Researchers at Ludwig Maximilians University and the Max Planck Institute of Quantum Optics have found a way to achieve this earlier this year. They created a quantum gas using potassium atoms near absolute zero. The atoms were confined in a lattice using a magnetic field and lasers such that there was an upper and lower bound on the allowed energies of the system. By altering the magnetic field and lasers they changed the repulsive force the atoms exerted on each other suddenly into attractive force. However, the specific conditions meant that it was energetically favourable for the atoms to maintain their lattice positions despite the reversal in the direction of the intermolecular force. Thus the system’s atoms preferentially occupied a high energy state meaning that its absolute temperature was negative. You can read more about this in their paper [1].
References:
[1] Braun S, Ronzheimer JP, Schreiber M, Hodgman SS, Rom T, Bloch I, Schneider U. 2013. Negative Absolute Temperature for Motional Degrees of Freedom. Science. 339 (6115): 52-55.
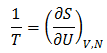
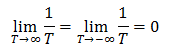
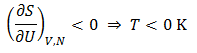
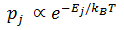
 RSS Feed
RSS Feed