In this article, I examine the kinetics by which chemical reactions approach completion or equilibrium. I illustrate how the reaction order, reversibility, and rate constants are all important variables. Additionally, I derive time-dependent equations for the reaction quotient of reversible reactions.
Irreversible first-order reaction
We begin with the simplest case: an irreversible first-order reaction. That is, a reaction where a single reactant (A) is converted into a single product (B). The rate is described by the first-order rate constant kf. Since the reaction is irreversible, conversion of product (B) back to reactant (A) does not occur. This process can be represented by the scheme:
The rate of formation of the product (B) is dependent on the rate constant (Kf) and the concentration of starting material (A). Thus, we can write this relationship as a differential equation:
Solving the differential equation requires the initial concentrations of A and B. I define the initial concentration of starting material as [A]0 and assume the initial product concentration to be zero. The solution to the differential equation gives the concentrations of A and B as a function of time.
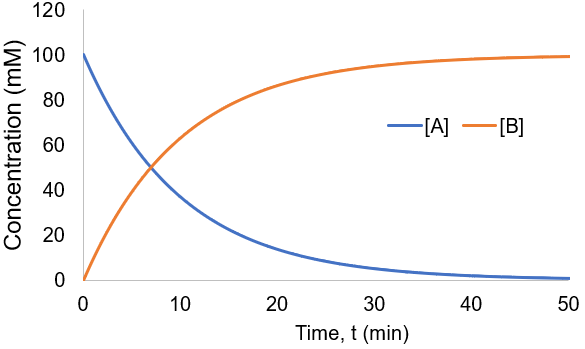
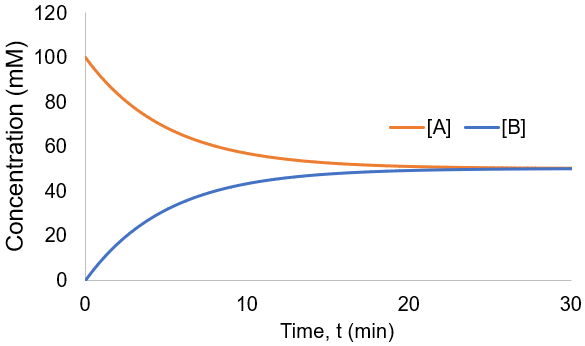
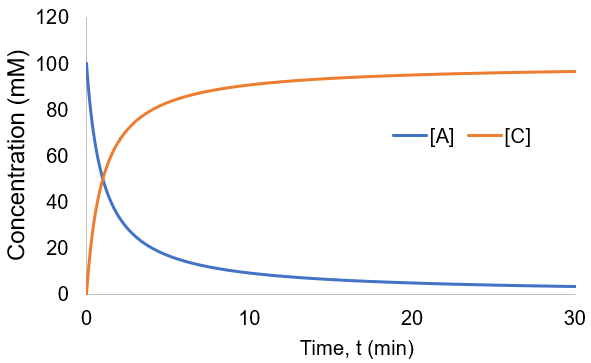
To visualize this kinetic profile, I plot [A] and [B] given [A]0 = 100 mM and Kf = 0.1 /min.
The reaction speed slows down over time as the concentration of A falls. This reaction is irreversible, so it is complete when all starting material (A) is converted to product (B). Stated differently, the system has reached equilibrium when all A has been converted to B. Thus, we can write:
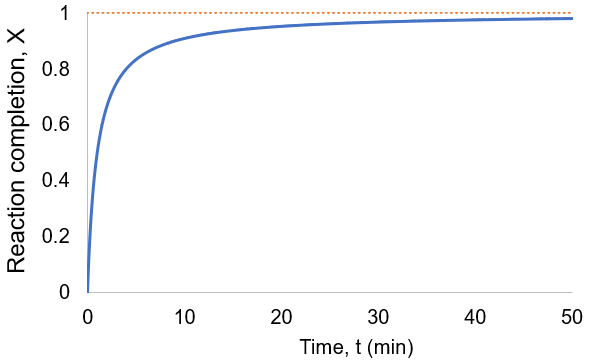
To quantify reaction progress, I define the reaction completion (X) as the ratio of the current product concentration to the concentration at equilibrium (when the reaction is fully complete):
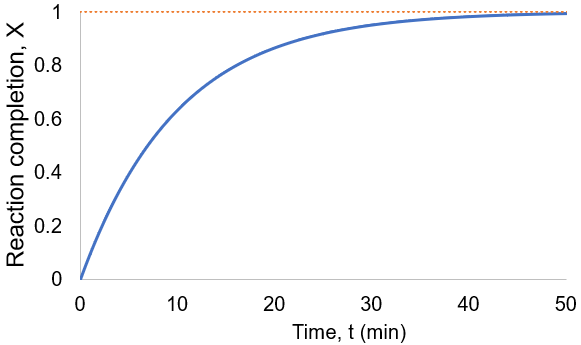
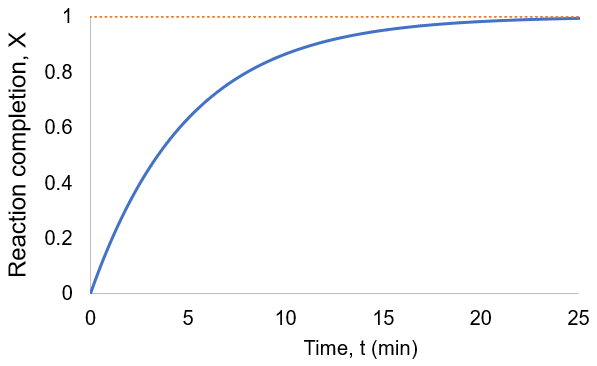
To visualize this, I plot reaction completion over time for the above case of kf = 0.1 /min:
We can see that this reaction (and all others we may consider) never truly reaches completion. Instead, the equilibrium state (X = 1) is infinitesimally approached. Therefore, chemical reactions are never 100% finished. However, pragmatically, we ought to call a reaction done when it is very close to finished. For instance, we could choose 99% as the limit. Solving the above equation, we can find the completion time (t) as a function of completion (X):
Completion time is dependent on the rate constant kf, with a faster rate giving quicker completion. Importantly, the completion time is independent of the starting reactant concentration. This is because it is a first-order process.
Reversible first-order reaction
Next, I consider a more general version of the previous scenario, making the first-order reaction reversible. As before the substrate (A) is converted to product (B) by first-order rate constant kf. Additionally, we now have the reverse reaction where B is converted to A by rate constant kr:
Expressing these kinetics as a differential equation, we require terms for both the forward and reverse processes.
To simply the mathematics, I assume that the initial concentration of product (B) is zero. Solving this differential equation:
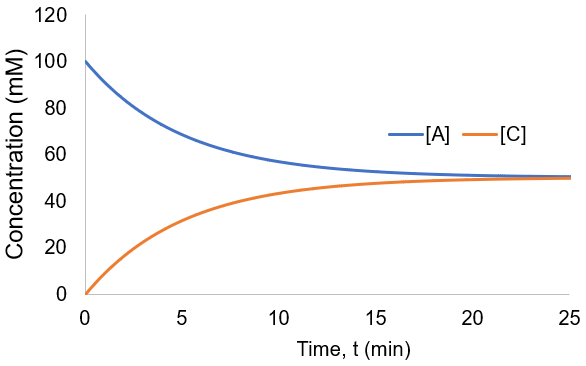
To visualize these kinetics, I plot [A] and [B] assuming [A]0 = 100 mM, and kf = kr = 0.1 /min.
Instead of all A being converted to B as in the irreversible case, an equilibrium is established between A and B depending on the relative size of the rate constants. We can derive an expression for the equilibrium concentrations by finding when their rate of change is zero:
Using these equilibrium concentrations, we can compute the reaction completion (X) as the ratio of the current product concentration to the concentration at equilibrium:
I plot reaction completion for the above scenario, where [A]0 = 100 mM, and kf = kr = 0.1 /min:
We have the same curve shape as in the irreversible case. Reaction completion is infinitesimally approached, but the reversible case has shorter completion time as the progress depends on the sum of forward and reverse rate constants rather than just the forward constant. Here, completion involves reaching equilibrium rather than consuming all starting material. Increasing either rate constant results in faster equilibration.
We can solve for completion time (t) as a function of reaction completion (X):
We can solve for completion time (t) as a function of reaction completion (X):
This equation takes on the same form as the irreversible case, adding the rate constant for the reverse reaction. A corollary of this is that given the same forward rate constant, the presence of the reverse reaction shortens the time to reach equilibrium.
For reversible reactions, another way to quantify progress is to compare the reaction quotient (Q) to the equilibrium constant (Keq). The reaction quotient takes the same form as the equilibrium constant, but uses the time-dependant concentrations:
For reversible reactions, another way to quantify progress is to compare the reaction quotient (Q) to the equilibrium constant (Keq). The reaction quotient takes the same form as the equilibrium constant, but uses the time-dependant concentrations:
We can derive a time-dependent equation for the reaction quotient by substituting the expressions for the concentrations:
The reaction quotient can be compared to the equilibrium constant by taking the ratio:
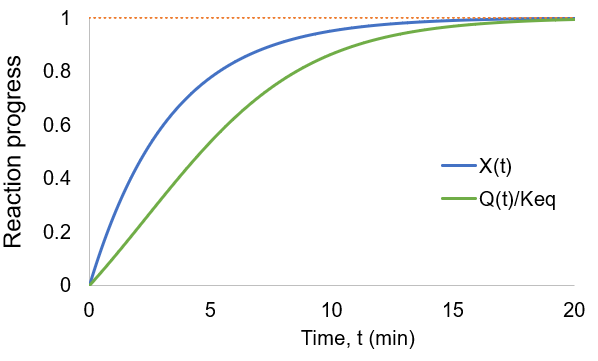
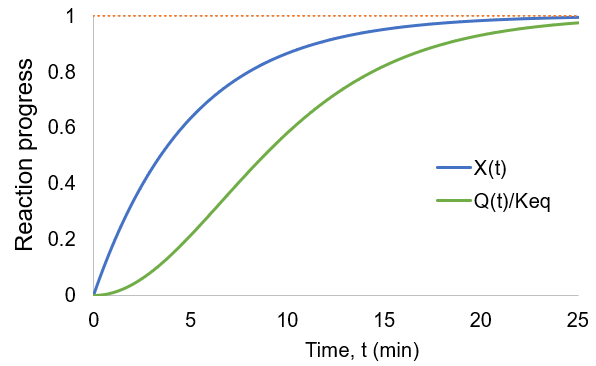
As the reaction proceeds the reaction quotient moves toward the equilibrium constant. When totally complete the ratio equals unity. To compare the reaction quotient (Q) and reaction completion (X) as measures of reaction progress, I calculate X(t)and Q(t)/Keq where [A]0 = 100 mM, kf = 0.2/min, and kr = 0.1 /min:
We can see that reaction completion and the reaction quotient give different curve shapes. These functions both measure reaction progress, each plateauing at unity when the reaction is finished. However, I believe that reaction completion is a more intuitive quantity, it is directly proportional to product concentration. Here is the mathematical relation between these concepts:
Irreversible second-order reaction
Many chemical reactions involve two molecules colliding, a bimolecular reaction. Suppose that starting materials A and B react to give products C and D. The reaction proceeds with forward second order rate constant Kf and is irreversible, following this kinetic scheme:
For simplicity, I assume that the starting concentrations and A and B are equal and there is initially no C and D. Thus, we can write the differential equation:
Solving the differential equation:
To visualize these kinetics, I plot [A] and [B] assuming [A]0 = 100 mM, and kf = 0.01 mM/min.
Compared to the first-order reactions considered above there is a dramatic slowing of the reaction progress when it is nearly complete. This behavior is a consequence of the reaction requiring the collision of reactants A and B: it becomes increasingly unlikely as their concentrations fall. In this scenario the reaction completion (X) as a function of time (t) given by:
Here is a plot of reaction completion for [A]0 = 100 mM, and kf = 0.01 mM/min:
This plot gives an even clearer visual indication of how second-order reactions become slow at low reactant concentrations. Solving for completion time (t) as a function of reaction completion (X):
Importantly, unlike for first-order reaction kinetics, the completion time is dependent on the initial substrate concentration. Collisions are more likely at higher concentrations, resulting in faster reaction rates.
Reversible second-order reaction
As a final case study, I make the second-order reaction reversible. As before, starting materials A and B react to give products C and D. Now in addition to the forward second order rate constant kf we have the reverse rate constant kr.
The reaction rate is given by the difference between the forward and reverse reactions. This system is simplified by assuming [C] = [D] = 0 at t = 0 and [A] = [B]. Thus, we can write:
Unfortunately, the solution to this differential equation is impractically complex (though analytically solvable). Numerical methods would be needed. Luckily, we can get an algebraic solution by taking the special case where the forward and reverse rate constants are equal:
To visualize these kinetics, I plot [A] and [B] assuming [A]0 = 100 mM, and k = 0.001 mM/min.
The reaction proceeded toward an equilibrium where [A] = [B] = [C] = [D] since the forward and reverse rate constants are equal. Note also that the reaction proceeds to equilibrium more uniformly then was seen in the irreversible case. This is because as the forward rate slows the reverse rate increases until they are equal. In this case, the reaction completion (X) as function of time (t) is:
We can also solve for completion time:
Like the other second-order reaction considered above, the completion is dependent on the initial substrate concentration. Additionally, since this is a reversible reaction, it results in an equilibrium and can also described by a reaction quotient:
In this case, since the forward and reverse rate constants are equal, the equilibrium constant is unity and reaction quotient is equal to the ratio of Q(t)/Keq:
Now, as for the unimolecular reversible reaction scenario, I compare reaction completion and the reaction progress as measures of reaction completion, assuming [A]0 = 100 mM, and k = 0.001 mM/min:
As before, both reaction completion and reaction quotient approach unity as the reaction progresses. However, the curve shapes are quite different. For instance, reaction completion increases at the maximum rate at the beginning of the reaction while the reaction quotient increases fastest in the middle of the reaction.
Summary: reaction order, reversibility, and completion time
Having explored several common schemes for first and second order chemical reactions, we can now compare their kinetics and how they approach completion. In the table below I compare each scenario’s completion time and the ratio of how long it takes for 50% completion versus 99% (t0.99/t0.5). This ratio provides information about the curve shape.
Whereas first-order processes are independent of starting concentration, second-order processes are faster under more concentrated conditions. Irreversible second-order reactions are further distinguished by how they dramatically slow down at high completion levels. While the other cases take 6.64 times the half-life to achieve 99% completion, second order irreversible reactions take 99 times the half-life. This is due to the sensitivity of second-order processes to concentration. The effect is not seen for symmetric second order reversible reactions because the declining forward rate is balanced with an increasing reverse rate.
Avogadro’s limit and absolute reaction completion
Throughout this article a central premise has been that chemical reactions never really reach completion, they only infinitesimally approach it. This is true from the mathematics, but considering the molecular nature of chemical reactions provides an alternative (though pedantic) way of viewing this. A chemical reaction is certainly complete when there is not a single molecule of starting material left. Avogadro’s number provides a lower limit on what chemical concentrations are possible (Avogadro’s limit). For instance, since there are 6.022 * 10^23 molecules in a mole, a solution of 1.66 × 10^-24 mol/L has exactly 1 molecule per litre of solution. For instance, consider an irreversible reaction with 1 L volume. If the reactant concentration falls below 1.66 × 10^-24 mol/L, there is no molecules left and it can be considered truly complete. We need to consider both the solution volume and Avogadro’s number to determine the concentration below which no molecules remain. Additionally, since the law of large numbers no longer applies, solutions near Avogadro’s limit need to be treated probabilistically. I discuss this topic in greater detail in my article on Avogadro’s limit. This idea can also be applied to reversible reactions. In this case, when the difference between the reactant and product concentrations and their theoretical equilibrium levels corresponds to less than one molecule, the reaction could be considered absolutely complete. Nonetheless, this sense of completion is not a very practical or useful one. Avogadro’s number is enormous, waiting for literally all molecules to be consumed is far too rigorous. We ought to consider a reaction very close to complete the same as complete.
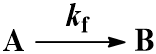
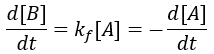
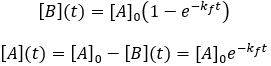
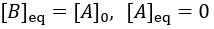
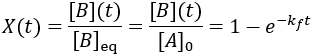
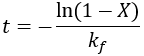
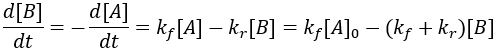
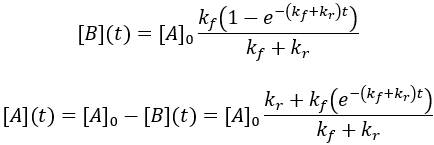
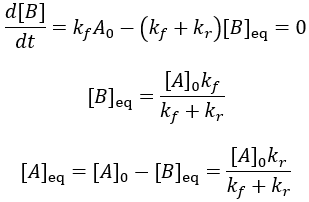
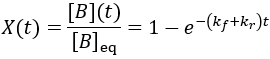
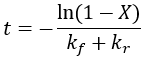

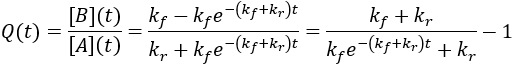
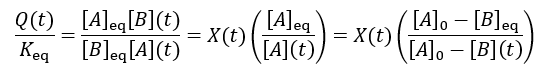
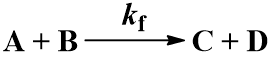
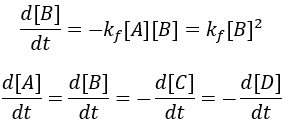
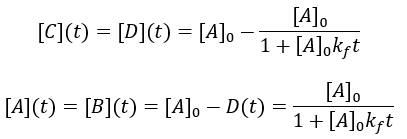
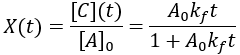
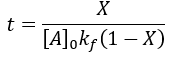
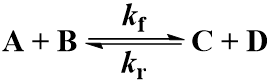
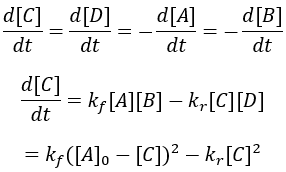
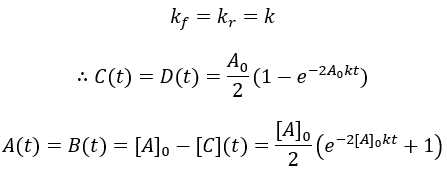
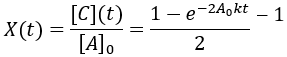
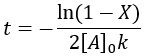
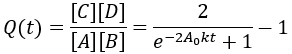
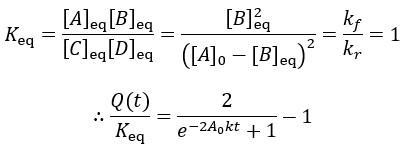

 RSS Feed
RSS Feed