The goal of this article is to fully categorize all ways in which things can exist. The most obvious type of this is physical existence. Such things exist at a particular location in three-dimensional space, have certain physical properties, and so forth. In essence, they are material. This is usually what is meant implicitly by the term “existence”.
Virtual existence
Thoughts and ideas exist in some manner, but not directly physically. We can call this virtual existence. For instance information stored in a book, digitally, or via our thoughts. A possible criticism of this classification would be that all of these methods of storing information are physical, and thus virtual existence may ultimately just be physical existence. It is true that the information must be stored somehow and this would be physical. However, physical existence refers explicitly to the material reality of an object. In contrast, virtual existence refers to the meaning derived from the information content stored. Thus these types of existence are distinct, although physical existence may be required as a medium to store the information for virtual existence.
Another possibility is things which in principle could exist physically or virtually but do not presently. We can call this potential existence. The class can be further divided into potential physical, potential virtual, or complete potential existence. Certain types of things are limited in what types of potential existence are available to them. For instance, an abstract concept could never exist physically so could only have potential virtual or virtual existence. In contrast, objects can exist physically or be conceived of. Thus they have all types of potential existence available to them. While I am presenting the categories of existence separately, some are not mutually exclusive. For instance, consider an object which does not yet exist physically. If imagined this object would have both virtual existence and potential physical existence.
The relationship between meaning and information becomes important when thinking about potential existence. It could be argued that all possible things which could exist virtually actually already do. That is, that there is no potential existence, everything which can exist virtually already does. Consider a set of information, such as the sequence of characters in a book. Given an appropriate decoder (such as our brain’s knowledge of language) this information can be translated into meaning as we read it. However, if we were to use a different decoder the meaning we extract would surely be different. The same strings of characters would be converted to a different set of meanings. There are truly infinite possibilities for how we might define a decoder, and thus all possible meanings could in principle be obtained from a given source of information. This could lead some to conclude that all things which could exist virtually already do, that there is nothing with potential virtual existence. As long as we choose the appropriate decoder for the information we could obtain any desired virtually-existing thing. However, thinking of meaning in this way leads to some absurd conclusions. All sets of information would content all possible meanings, regardless of if any were considered when the information was recorded. Even things as simple as the letter “A” would encode all meanings possible. Clearly it is not reasonable to think about the meaning held by a given set of information this way. Instead, it is more sensible to use only the intended decoder that the information was originally recorded with respect to. We should consider a piece of information’s meaning only that which was intended. Potential existence is therefore a valid concept; there surely are many things which could exist virtually but have not been conceived yet.
Non-existence
We can define all of the previous types of existence as members of the set of real existence. Imagine now that there are some ideas or objects which are logically impossible and thus cannot have real existence. However, its absence from the real existence set could be seen as a type of existence in itself. I refer to this as non-existence. By its nature it is uniquely difficult to give examples of this type of existence since any must be necessarily inconceivable. If you could imagine it then it is actually an example of virtual existence. It is possible to construct examples, though we cannot imagine them. This can be done by considering things which contain self-contradictions. For instance, try to picture a triangle that has four sides or a square with three. These examples are absurd; by definition triangles have three sides while squares have four. If we tried to draw a triangle with four sides we would end up with a square, not a triangle. Both impossible shapes can be considered to belong to the non-existence set. Combining mutually exclusive properties in the same object is a general route to define something non-existing, since it introduces self-contradiction. It is bizarre to think of the impossibility of something existing as a type of existence itself. The situation gets even stranger, however, if we consider contradiction with respect to something’s existence type itself. For instance, suppose we take a non-existing object and also assume simultaneously that it has the property of real existence. By definition real and non-existence are mutually exclusive. Thus an object which has both real and non-existence is impossible, it belongs to the set of non-existence. In other words, the union of the non-existence and real existence sets is itself non-existing. Note that there may be many properties beyond self-contradiction which result in non-existence. The purpose of my examples is only to illustrate that there exists a class of things which are non-existing.
The solutions to certain problem may also belong to the non-existing set. For instance, consider the classical logical paradox: this statement is false. The statement claims that it is false, but if it was then it would actually be true. There appears to be no solution to this problem since contradiction arises in either case. However, we can actually consider there to be a solution which belongs to the non-existing set. Imagine that a third state is possible, that the statement could simultaneously be both true and false. This itself is contradictory, but recall that self-contradiction is allowed in the non-existence set. This answer resolves the paradox: if it is both true and false at the same time then it can be true that the statement is false.
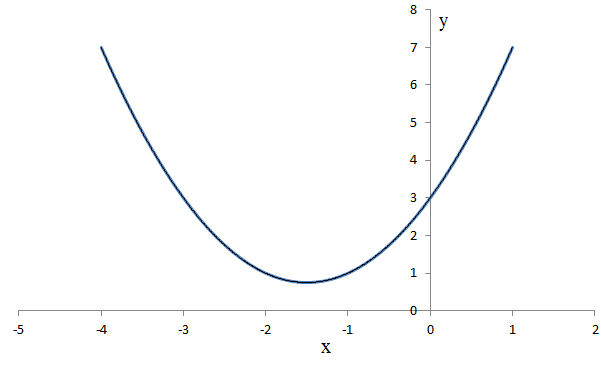
Interestingly, the notion I have developed here of non-existence already exists in mathematics. This is through the use of imaginary numbers. These contain "i", which is defined as the square root of -1. The solution to the square root operator must, when squared, give the original number whose square root was taken. If we square 1, we get 1. If we square -1, we also get 1 since the two negatives cancel. Thus there are no real numbers which satisfy this. However, in mathematics the imaginary number i is defined to be the number which has this property. Imaginary numbers must therefore belong to the non-existing set. This is because their logically impossible nature prohibits them from belonging to the real existence set. To better understand the meaning of imaginary numbers, consider the quadratic equation:
The consideration of non-existence as a valid type of existence may seem unnecessary and useless. Interestingly though, imaginary numbers in mathematics have been found to be extremely helpful. Their use is able to simplify the solving of some types of differential equations, particularly in the field of electrical engineering. The notion of non-existence that I presented here can be seen as a generalized version of the imaginary number. A question naturally follows this realization: since imaginary numbers are useful for some types of mathematics, is the concept of non-existence useful in any areas within logic or philosophy? I have yet to realize any analogous uses of this notion to simplify problems in these fields. Nevertheless, the possibility is intriguing. I leave finding such an application as an open problem for the reader.
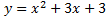
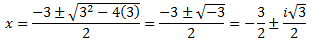
 RSS Feed
RSS Feed